题目内容
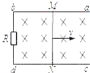
【题目】如图所示为一“匚”字型金属框架截面图，上下为两水平且足够长平行金属板，通过左侧长度为L＝1m的金属板连接。空间中有垂直纸面向里场强大小B＝0.2T的匀强磁场，金属框架在外力的作用下以速度v0＝1m/s水平向左做匀速直线运动。框架内O处有一质量为m＝0.1kg、带正电q＝1C的小球。若以某一速度水平向右飞出时，则沿图中虚线
′做直线运动；若小球在O点静止释放，则小球的运动轨迹沿如图曲线（实线）所示，已知此曲线在最低点P的曲率半径（曲线上过P点及紧邻P点两侧的两点作一圆，在极限情况下，这个圆的半径叫做该点的曲率半径）为P点到O点竖直高度h的2倍，重力加速度g取10 m/s2。求：
（1）小球沿图中虚线做直线运动速度v大小
（2）小球在O点静止释放后轨迹最低点P到O点竖直高度h
【答案】（1）
；（2）
【解析】
解：(1)框架向左运动，产生感应电动势：
板间场强：
小球做匀速直线运动，受力平衡：
可解得：
(2)最大速率点在轨迹的最低点
根据动能定理可得：
最低点根据牛顿第二定律和圆周运动规律有：
联立可解得：
练习册系列答案
相关题目
