Question

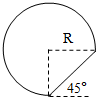
如图所示，由倾角45°光滑斜面和半径为R的

3

4

光滑圆周组成的轨道固定在竖直平面内，斜面和圆周之间有小圆弧平滑连接．一小球以一定的初速度释放，始终贴着轨道内侧顺时针转动，已知重力加速度为g则其通过斜面的时间最长可能是多少？

Answer 1

小球在最高点的速度最小时，通过斜面的时间最长．根据mg=m

v12

R

得：v1=

gR

，
设到达斜面顶端的速度为v₂，根据动能定理得：
mgR=

1

2

mv22-

1

2

mv12
解得：v₂=

3gR

．
小球在斜面上运动的加速度为：a=

mgsin45°

m

=

2

2

g
根据

2

R=v2t+

1

2

?

2

2

gt2
得：t=

5gR - 3gR

2 2 g

．
答：通过斜面的时间最长可能是

5gR - 3gR

2 2 g

．