题目内容
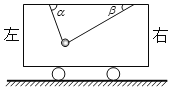
【题目】某电动机工作时输出功率P与拉动物体的速度v之间的关系如图所示。现用该电动机在水平地面内拉动一物体(可视为质点),运动过程中轻绳始终处在拉直状态,且不可伸长,如图所示。已知物体质量m=1kg,与地面的动摩擦因数μ1=0.35,离出发点左侧s距离处另有一段动摩擦因数为μ2、长为d的粗糙材料铺设的地面。(g取10m/s2)
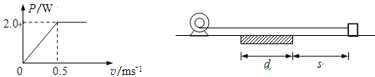
(1)若s足够长,电动机功率为2W时,物体在地面能达到的最大速度是多少?
(2)在μ1=0.35的水平地面运动,当物体速度为0.1m/s时,加速度为多少?
(3)若s=0.16m,物体与粗糙材料之间动摩擦因数μ2=0.45。启动电动机后,分析物体在达到粗糙材料之前的运动情况。若最终能以0.1m/s速度滑过粗糙材料,则d应为多少?
【答案】(1)4/7m/s;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)物体达到最大速度时,加速度为零,此时牵引力等于阻力,根据P=Fv求解最大速度;(2)根据P=Fv求解牵引力,根据牛顿第二定律求解加速度;(3)根据牛顿第二定律结合运动公式分析物体的运动情况.
(1)电动机拉动物体后,水平方向受拉力F和摩擦力f1
f1=μ1N,N=mg,f1=3.5N
物体速度最大时,加速度为零,F1=f1
根据P=Fv,vm=P/F1= P/f1,vm=![]() m/s
m/s
(2)当v=0.1m/s时,由图像及P=Fv可知,拉力F2= P/v= 4N
由牛顿第二定律F =ma F2 - f1=ma1
解得a1=0.5m/s2
(3)由(2)知,物体在速度达到0.5m/s前,拉力F恒定,物体做初速为零的匀加速直线运动。a1=0.5m/s2
速度达到v1=0.5m/s时,应经过s’= v12/2a1=0.25m>0.16m
所以小物体一直做匀加速运动到达粗糙材料,到达粗糙材料时速度v1=![]() =0.4m/s
=0.4m/s
在粗糙材料上运动时, f2=μ2N,N=mg,f2=4.5N
由牛顿第二定律 F2 -f2 =ma2,a2=-0.5m/s2
小物体停止前最多滑行d2=v22- v12/2a2=0.15m