题目内容
如图所示，电源电动势为E=100V，内阻不计，R1、R2、R4的阻值均为300Ω，R3为可变电阻．C为一水平放置的平行板电容器，虚线到两极板距离相等且通过竖直放置的荧光屏中心，极板长为L=8cm，板间距离为d=1cm，右端到荧光屏距离为s=20cm，荧光屏直径为D=5cm．有一细电子束沿图中虚线以E=9.6×102eV的动能连续不断地向右射入平行板电容器．已知电子电量e=1.6×1019C．要使电子都能打在荧光屏上，变阻器R3的取值范围多大？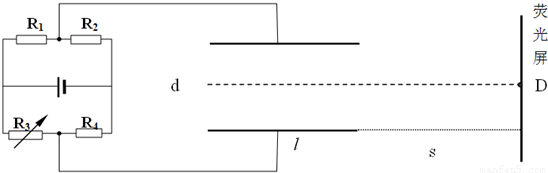
【答案】分析：带电粒子垂直进入电压可调的两平行板运动，在电场力作用下做类平抛运动，由荧光屏的宽度可确定粒子的偏转位移，从而求出两平行板间的电压，再由闭合电路殴姆定律可得使电子都能打在荧光屏上，变阻器R3的取值范围．
解答：解：
电子穿过电容器过程中，在水平方向上做匀速运动 l=vt①
在竖直方向上做匀加速直线运动
②
v⊥=at ③
a=
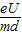④
电子穿过平行板电容器时，速度方向偏转θ角，tanθ=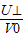
⑤
电子打在荧光屏上偏离中心O的位移，y=y1+s?tanθ
由上述①～⑥方程得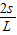：y=（1+
）y1
当y1=
d时，代入数据求得：y=3m＞
⑦
故使电子打在荧光屏上，应满足y≤
阶段
联立①～⑦方程，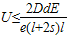
代入数据求得，A、B间电压U≤25V
（1）当UAB=25V时，
代入数据得：R3=900Ω
（2）当UBA=25V时，
代入数据得：R3=100Ω
综述：100Ω≤R3≤900Ω
点评：粒子进入电场后做类平抛运动，将运动分解两个方向的简单直线运动，从而确定侧向位移，最终得出AB板间的电压．
解答：解：
电子穿过电容器过程中，在水平方向上做匀速运动 l=vt①
在竖直方向上做匀加速直线运动
②v⊥=at ③
a=
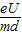④电子穿过平行板电容器时，速度方向偏转θ角，tanθ=
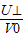⑤电子打在荧光屏上偏离中心O的位移，y=y1+s?tanθ
由上述①～⑥方程得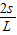：y=（1+
）y1当y1=
d时，代入数据求得：y=3m＞ ⑦故使电子打在荧光屏上，应满足y≤
阶段 联立①～⑦方程，
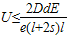
代入数据求得，A、B间电压U≤25V
（1）当UAB=25V时，
代入数据得：R3=900Ω
（2）当UBA=25V时，
代入数据得：R3=100Ω
综述：100Ω≤R3≤900Ω
点评：粒子进入电场后做类平抛运动，将运动分解两个方向的简单直线运动，从而确定侧向位移，最终得出AB板间的电压．
练习册系列答案
相关题目
（2011?静安区一模）如图所示，电源电动势E=50V，内阻r=1Ω，R1=30Ω，R2=60Ω．间距d=0.2m的两平行金属板M、N水平放置，闭合开关S，板间电场视为匀强电场．板间竖直放置一根长也为d的光滑绝缘细杆AB，有一个穿过细杆的带电小球p，质量为m=1×10-2kg、电荷量为q=+1×10-3C（可视为点电荷，不影响电场的分布），现将小球p从杆的顶端A处由静止释放，小球p沿杆向下运动到杆的中点O时，速度为v=2m/s．求：
如图所示，电源电动势为E，内电阻为r．当滑动变阻器的触片P从右端滑到左端时，发现电压表V1、V2示数变化的绝对值分别为△U1和△U2，下列说法中正确的是（ ）
如图所示，电源电动势为E，内电阻为r．两电压表可看作是理想电表，当闭合开关，将滑动变阻器的触片由右端向左滑动时，下列说法中正确的是（ ）
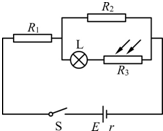如图所示，电源电动势为E，内电阻为r，L为小灯泡（其灯丝电阻可视为不变），R1和R2为定值电阻，R3为光敏电阻，其阻值的大小随照射光强度的增强而减小．闭合开关S后，将照射光强度增强，则（ ）| A、电路的路端电压将增大 | B、灯泡L将变暗 | C、R1两端的电压将增大 | D、内阻r上发热的功率将增大 |
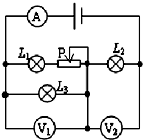如图所示，电源电动势为E，内电阻为r，当滑动变阻器的触片P从右端滑到左端时，发现电压表V1、V2示数为U1、U2，示数变化的绝对值分别为△U1和△U2，电流表的示数为I，电流表示数变化的绝对值为△I，下列说法中正确的是（ ）| A、小灯泡L1、L2变暗，L3变亮 | ||||
| B、小灯泡L3变暗，L1、L2变亮 | ||||
| C、△U1＜△U2 | ||||
D、
|