题目内容
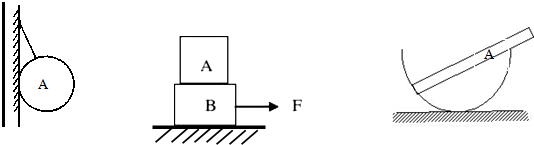
3. 如图,在水平地面上固定一倾角为θ的光滑绝缘斜面,斜面处于电场强度大小为E、方向沿斜面向下的匀强电场中.一劲度系数为k的绝缘轻质弹簧的一端固定在斜面底端,整根弹簧处于自然状态.一质量为m、带电量为q(q>0)的滑块从距离弹簧上端为S0处静止释放,滑块在运动过程中电量保持不变,设滑块与弹簧接触后粘在一起不分离且没有机械能损失,物体刚好返回到S0段中点,弹簧始终处在弹性限度内,重力加速度大小为g.则( )
如图,在水平地面上固定一倾角为θ的光滑绝缘斜面,斜面处于电场强度大小为E、方向沿斜面向下的匀强电场中.一劲度系数为k的绝缘轻质弹簧的一端固定在斜面底端,整根弹簧处于自然状态.一质量为m、带电量为q(q>0)的滑块从距离弹簧上端为S0处静止释放,滑块在运动过程中电量保持不变,设滑块与弹簧接触后粘在一起不分离且没有机械能损失,物体刚好返回到S0段中点,弹簧始终处在弹性限度内,重力加速度大小为g.则( )| A. | 滑块从静止释放到与弹簧上端接触瞬间所经历的时间为t=$\sqrt{\frac{2m{S}_{0}}{qE+mgsinθ}}$ | |
| B. | 滑块运动过程中的最大动能等于(mgsinθ+qE)($\frac{mgsinθ}{k}$+S0) | |
| C. | 弹簧的最大弹性势能为(mgsinθ+qE)($\frac{2mgsinθ+2qE}{k}$+$\frac{3{S}_{0}}{2}$) | |
| D. | 运动过程中地球、物体和弹簧组成系统的机械能和电势能总和始终不变 |
分析 根据牛顿第二定律求解出加速度,然后结合运动学公式求出滑块从静止释放到与弹簧上端接触瞬间所经历的时间.当滑块的合力为零时动能最大.结合功能原理逐项列式分析即可.
解答 解:A、滑块从静止释放到与弹簧刚接触的过程中做初速度为零的匀加速直线运动,设加速度大小为a,则有
qE+mgsinθ=ma,S0=$\frac{1}{2}$at2
联立可得:t=$\sqrt{\frac{2m{S}_{0}}{qE+mgsinθ}}$,故A正确
B、滑块速度最大时受力平衡,设此时弹簧压缩量为x0,则有mgsinθ+qE=kx0
从静止释放到速度达到最大的过程中,由动能定理得
(mgsinθ+qE)•(S0+x0)+W=Ekm-0
由于弹簧弹力做负功,故最大动能Ekm<(mgsinθ+qE)•(S0+x0)=(mgsinθ+qE)($\frac{mgsinθ}{k}$+S0),故B错误;
C、滑块与弹簧接触后粘在一起后做简谐运动,振幅为 A=$\frac{1}{2}$S0+x0,则滑块向下运动时弹簧的最大压缩量为 xm=x0+$\frac{1}{2}$S0+x0=2x0+$\frac{1}{2}$S0
当弹簧压缩量最大时,弹性势能最大,即Epm=(mgsinθ+qE)(S0+x0)=(mgsinθ+qE)(S0+2x0+$\frac{1}{2}$S0)=(mgsinθ+qE)($\frac{2mgsinθ+2qE}{k}$+$\frac{3{S}_{0}}{2}$),故C正确;
D、物体运动过程中只有重力和电场力做功,故地球、物体和弹簧组成系统的机械能和电势能总和不变,故D正确;
故选:ACD
点评 本题是含弹簧问题,由于弹簧的弹力是变力,滑块是变加速运动,滑块与弹簧接触后粘在一起后做简谐运动,要抓住简谐运动的对称性分析弹簧的压缩量,结合功能关系解答.

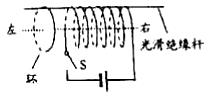 我国未来航母上飞机弹射起飞可以利用电磁驱动来实现.电磁驱动原理如图所示.当固定线圈上突然通过直流电流时,线圈端点的金属环被弹射出去.现在固定线圈左侧同一位置,先后放有分别用横截面积相等的铜和铝导线制成形状、大小相同的两个闭合环,且电阻率ρ铜<ρ铝.合上开关S的瞬间( )
我国未来航母上飞机弹射起飞可以利用电磁驱动来实现.电磁驱动原理如图所示.当固定线圈上突然通过直流电流时,线圈端点的金属环被弹射出去.现在固定线圈左侧同一位置,先后放有分别用横截面积相等的铜和铝导线制成形状、大小相同的两个闭合环,且电阻率ρ铜<ρ铝.合上开关S的瞬间( )| A. | 从左侧看环中感应电流沿顺时针方向 | |
| B. | 铜环受到的安培力大于铝环受到的安培力 | |
| C. | 若将铜环放置在线圈右方,环将向左运动 | |
| D. | 电池正负极调换后,金属环仍能向左弹射 |
 利用传感器与计算机结合,可以绘制出物体运动的图象,某同学在一次实验中得到一沿平直轨道运动小车的速度一时间图象如图所示,由此图象可知( )
利用传感器与计算机结合,可以绘制出物体运动的图象,某同学在一次实验中得到一沿平直轨道运动小车的速度一时间图象如图所示,由此图象可知( )| A. | 小车在20s-40s做加速度恒定的匀变速直线运动 | |
| B. | 20s末小车回到出发点 | |
| C. | 小车10-30s内的加速度方向相同 | |
| D. | 小车0-10s内的平均速度小于10-20s内的平均速度 |
| A. | 在高大的建筑物顶端安装的避雷针是利用尖端放电避免雷击的一种设施 | |
| B. | 超高压带电作业的工人穿戴的用包含金属丝织物制成的工作服可以起到静电屏蔽的作用 | |
| C. | 法拉第首先提出了电荷周围存在电场的观点 | |
| D. | 安培通过实验发现了电流的磁效应,首次揭示了电与磁的联系 |
 如图所示,半径为R的质量为m的光滑球体,静止在桌边和墙边.已知:桌边缘与墙面的距离为d.
如图所示,半径为R的质量为m的光滑球体,静止在桌边和墙边.已知:桌边缘与墙面的距离为d.