题目内容
 (2013?淮安模拟)如图所示,倾角为37°的粗糙斜面AB底端与半径R=0.4m的光滑半圆轨道BC平滑相连,O为轨道圆心,BC为圆轨道直径且处于竖直方向,A、C两点等高.质量m=1kg的滑块从A点由静止开始下滑,恰能滑到与O等高的D点,g取10m/s2,sin37°=0.6,cos37°=0.8.
(2013?淮安模拟)如图所示,倾角为37°的粗糙斜面AB底端与半径R=0.4m的光滑半圆轨道BC平滑相连,O为轨道圆心,BC为圆轨道直径且处于竖直方向,A、C两点等高.质量m=1kg的滑块从A点由静止开始下滑,恰能滑到与O等高的D点,g取10m/s2,sin37°=0.6,cos37°=0.8.(1)求滑块与斜面间的动摩擦因数μ.
(2)若使滑块能到达C点,求滑块从A点沿斜面滑下时的初速度v0的最小值.
(3)若滑块离开C处的速度大小为4m/s,求滑块从C点飞出至落到斜面上的时间t.
分析:(1)由题,滑块恰能滑到与O等高的D点,速度为零,对A到D过程,运用动能定理列式可求出动摩擦因数μ.
(2)滑块恰好能到达C点时,由重力提供向心力,根据牛顿第二定律列式可得到C点的速度范围,再对A到C过程,运用动能定理求初速度v0的最小值.
(3)离开C点做平抛运动,由平抛运动的规律和几何知识结合求时间.
(2)滑块恰好能到达C点时,由重力提供向心力,根据牛顿第二定律列式可得到C点的速度范围,再对A到C过程,运用动能定理求初速度v0的最小值.
(3)离开C点做平抛运动,由平抛运动的规律和几何知识结合求时间.
解答:解:(1)滑块由A到D过程,根据动能定理,有:
mg(2R-R)-μmgcos37°?
=0-0
得 μ=
tan37°=0.375
(2)若滑块能到达C点,根据牛顿第二定律 有 mg+FN=
则得 vc≥
=2m/s
A到C的过程:根据动能定理 有-μmgcos37°?
=
m
-
m
联立解得,v0=
≥2
m/s
所以初速度v0的最小值为2
m/s.
(3)滑块离开C点做平抛运动,则有
x=vct
y=
gt2
由几何关系得:tan37°=
联立得 5t2+3t-0.8=0
解得 t=0.2s
答:
(1)滑块与斜面间的动摩擦因数μ为0.375.
(2)若使滑块能到达C点,滑块从A点沿斜面滑下时的初速度v0的最小值为2
m/s.
(3)若滑块离开C处的速度大小为4m/s,滑块从C点飞出至落到斜面上的时间t是0.2s.
mg(2R-R)-μmgcos37°?
| 2R |
| sin37° |
得 μ=
| 1 |
| 2 |
(2)若滑块能到达C点,根据牛顿第二定律 有 mg+FN=
m
| ||
| R |
则得 vc≥
| Rg |
A到C的过程:根据动能定理 有-μmgcos37°?
| 2R |
| sin37° |
| 1 |
| 2 |
| v | 2 C |
| 1 |
| 2 |
| v | 2 0 |
联立解得,v0=
|
| 3 |
所以初速度v0的最小值为2
| 3 |
(3)滑块离开C点做平抛运动,则有
x=vct
y=
| 1 |
| 2 |
由几何关系得:tan37°=
| 2R-y |
| x |
联立得 5t2+3t-0.8=0
解得 t=0.2s
答:
(1)滑块与斜面间的动摩擦因数μ为0.375.
(2)若使滑块能到达C点,滑块从A点沿斜面滑下时的初速度v0的最小值为2
| 3 |
(3)若滑块离开C处的速度大小为4m/s,滑块从C点飞出至落到斜面上的时间t是0.2s.
点评:本题是动能定理与向心力、平抛运动及几何知识的综合,要注意挖掘隐含的临界条件,运用几何知识求解.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 (2013?淮安模拟)如图所示为一种质谱仪示意图,由加速电场、静电分析器和磁分析器组成.若静电分析器通道中心线的半径为R,通道内均匀辐射电场在中心线处的电场强度大小为E,磁分析器有范围足够大的有界匀强磁场,磁感应强度大小为B、方向垂直纸面向外.一质量为m、电荷量为q的粒子从静止开始经加速电场加速后沿中心线通过静电分析器,由P点垂直边界进入磁分析器,最终打到胶片上的Q点.不计粒子重力.下列说法正确的是( )
(2013?淮安模拟)如图所示为一种质谱仪示意图,由加速电场、静电分析器和磁分析器组成.若静电分析器通道中心线的半径为R,通道内均匀辐射电场在中心线处的电场强度大小为E,磁分析器有范围足够大的有界匀强磁场,磁感应强度大小为B、方向垂直纸面向外.一质量为m、电荷量为q的粒子从静止开始经加速电场加速后沿中心线通过静电分析器,由P点垂直边界进入磁分析器,最终打到胶片上的Q点.不计粒子重力.下列说法正确的是( )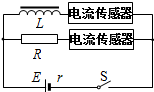 (2013?淮安模拟)如图所示,用电流传感器研究自感现象.电源内阻不可忽略,线圈的自感系数较大,其直流电阻小于电阻R的阻值.t=0时刻闭合开关S,电路稳定后,t1时刻断开S,电流传感器连接计算机分别描绘了整个过程线圈中的电流IL和电阻中的电流IR随时间t变化的图象.下列图象中可能正确的是( )
(2013?淮安模拟)如图所示,用电流传感器研究自感现象.电源内阻不可忽略,线圈的自感系数较大,其直流电阻小于电阻R的阻值.t=0时刻闭合开关S,电路稳定后,t1时刻断开S,电流传感器连接计算机分别描绘了整个过程线圈中的电流IL和电阻中的电流IR随时间t变化的图象.下列图象中可能正确的是( )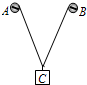 (2013?淮安模拟)如图所示,A、B为同一水平线上的两个绕绳装置,转动A、B改变绳的长度,使光滑挂钩下的重物C缓慢下降.关于此过程绳上拉力大小变化,下列说法中正确的是( )
(2013?淮安模拟)如图所示,A、B为同一水平线上的两个绕绳装置,转动A、B改变绳的长度,使光滑挂钩下的重物C缓慢下降.关于此过程绳上拉力大小变化,下列说法中正确的是( ) (2013?淮安模拟)如图所示,电压互感器、电流互感器可看成理想变压器,已知电压互感器原、副线圈匝数比是1000:1,电流互感器原、副线圈匝数比是1:200,电压表读数是200V,电流表读数是1.5A,则交流电路输送电能的功率是( )
(2013?淮安模拟)如图所示,电压互感器、电流互感器可看成理想变压器,已知电压互感器原、副线圈匝数比是1000:1,电流互感器原、副线圈匝数比是1:200,电压表读数是200V,电流表读数是1.5A,则交流电路输送电能的功率是( )