题目内容
(1)某同学在做“利用单摆测重力加速度”的实验时,有下列步骤,其中正确的是
A.取长度约1m的细线,一端固定在铁架台上,另一端栓一个小铁球
B.测出细线的长度即为单摆的摆长L
C.使小铁球离开其平衡位置约30cm的距离,将其静止释放
D.待小铁球摆动稳定后,当小铁球经过平衡位置时按下秒表开始计时
E.开始计时时记为1,当小铁球第50次经过平衡位置停止计时,所测时间为50个周期(t=50T)
(2)若某次测量时间结果如图所示,则秒表的读数是
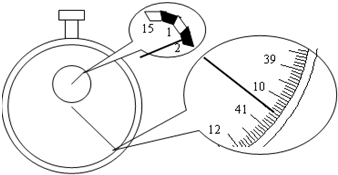
(3)若测出的g值较当地重力加速度的值偏大,可能原因是
A.小球的质量偏大
B.用摆线的长度当作摆长
C.将实际振动n次数误记为(n+1)次
D.摆线上端没有系牢,摆动过程因松动而使摆线变长.
AD
AD
(不定项)A.取长度约1m的细线,一端固定在铁架台上,另一端栓一个小铁球
B.测出细线的长度即为单摆的摆长L
C.使小铁球离开其平衡位置约30cm的距离,将其静止释放
D.待小铁球摆动稳定后,当小铁球经过平衡位置时按下秒表开始计时
E.开始计时时记为1,当小铁球第50次经过平衡位置停止计时,所测时间为50个周期(t=50T)
(2)若某次测量时间结果如图所示,则秒表的读数是
100.5
100.5
s.
(3)若测出的g值较当地重力加速度的值偏大,可能原因是
C
C
(不定项)A.小球的质量偏大
B.用摆线的长度当作摆长
C.将实际振动n次数误记为(n+1)次
D.摆线上端没有系牢,摆动过程因松动而使摆线变长.
分析:(1)用单摆测重力加速度实验的注意事项:摆长等于悬点到球心的距离;摆长约为1m左右;单摆在摆角较小时(小于5°)可看成简谐运动;摆球经过最低时开始计时,便于测量单摆的周期;
(2)秒表分子与秒针的示数之和是秒表的示数,由图示秒表可以读出秒表示数;
(3)根据单摆周期公式分析实验误差.
(2)秒表分子与秒针的示数之和是秒表的示数,由图示秒表可以读出秒表示数;
(3)根据单摆周期公式分析实验误差.
解答:解:(1)A、取长度约1m的细线,一端固定在铁架台上,另一端栓一个小铁球,符合实验要求,故A正确;
B、摆线长度与摆球半径之和是摆长,测出细线的长度作为单摆的摆长L是错误的,故B错误;
C、单摆的最大摆角应小于5°,小铁球离开其平衡位置约30cm的距离,将其静止释放,摆角太大,故C错误;
D、待小铁球摆动稳定后,当小铁球经过平衡位置时按下秒表开始计时,故D正确;
E、开始计时时记为1,当小铁球第50次经过平衡位置停止计时,所测时间为49个周期,不是50个周期,故E错误;
故正确的实验步骤是AD.
(2)由图示秒表可知,秒表的分针示数是1min=60s,秒针示数是40.5s,则秒表示数是60s+40.5s=100.5s.
(3)由单摆周期公式T=2π
可知,g=
;
A、由g=
可知,重力加速度与摆球质量无关,故A错误;
B、用摆线的长度当作摆长,摆长L偏小,由g=
可知,所测重力加速偏小,不符合题意,故B错误;
C、将实际振动n次数误记为(n+1)次,所测单摆周期T变小,由g=
可知,所测重力加速度偏大,符合题意,故C正确;
D、摆线上端没有系牢,摆动过程因松动而使摆线变长,由T=2π
可知.所测单摆的实际周期T偏大,由g=
可知所测重力加速度偏小,不符合题意,故D错误;
故答案为:(1)AD;(2)100.5;(3)C.
B、摆线长度与摆球半径之和是摆长,测出细线的长度作为单摆的摆长L是错误的,故B错误;
C、单摆的最大摆角应小于5°,小铁球离开其平衡位置约30cm的距离,将其静止释放,摆角太大,故C错误;
D、待小铁球摆动稳定后,当小铁球经过平衡位置时按下秒表开始计时,故D正确;
E、开始计时时记为1,当小铁球第50次经过平衡位置停止计时,所测时间为49个周期,不是50个周期,故E错误;
故正确的实验步骤是AD.
(2)由图示秒表可知,秒表的分针示数是1min=60s,秒针示数是40.5s,则秒表示数是60s+40.5s=100.5s.
(3)由单摆周期公式T=2π
|
| 4π2L |
| T2 |
A、由g=
| 4π2L |
| T2 |
B、用摆线的长度当作摆长,摆长L偏小,由g=
| 4π2L |
| T2 |
C、将实际振动n次数误记为(n+1)次,所测单摆周期T变小,由g=
| 4π2L |
| T2 |
D、摆线上端没有系牢,摆动过程因松动而使摆线变长,由T=2π
|
| 4π2L |
| T2 |
故答案为:(1)AD;(2)100.5;(3)C.
点评:本题考查了用单摆测重力加速度的实验操作、秒表读数、实验误差分析等问题;要掌握常用器材的使用及读数方法;实验误差分析是本题的难点,熟练应用单摆周期公式认真分析,是正确解题的关键.

练习册系列答案
相关题目


 B.
B. C.
C. D.
D.



 B.
B. C.
C. D.
D.

