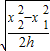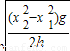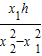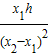题目内容
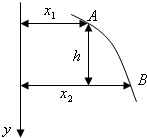
 某同学在做平抛实验中,在纸上记下了纵坐标y,描出了如图所示的一段曲线,忘记标出抛出点的位置.为了求得初速度,他在曲线上取A、B两点,并用刻度尺分别量出它们到y轴的距离x1、x2,以及AB的竖直距离h,则小球的初速度v0和落到A点时下落的竖直高度y0应为下面的( )
某同学在做平抛实验中,在纸上记下了纵坐标y,描出了如图所示的一段曲线,忘记标出抛出点的位置.为了求得初速度,他在曲线上取A、B两点,并用刻度尺分别量出它们到y轴的距离x1、x2,以及AB的竖直距离h,则小球的初速度v0和落到A点时下落的竖直高度y0应为下面的( )分析:平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,设初速度为v0,根据水平方向上的位移x1和x2,得出抛出点运动到A和B的时间,根据竖直方向上的距离差为h,求出初速度.
解答:解:设初速度为v0,则从抛出点运动到A所需的时间t1=
,从抛出点运动到B所需的时间t2=
,
在竖直方向上有:
gt22-
gt12=h,
代入t1、t2,解得:v0=
.
落到A点时下落的竖直高度y0=
gt12=
故B正确,A、C、D错误.
故选B.
| x1 |
| v0 |
| x2 |
| v0 |
在竖直方向上有:
| 1 |
| 2 |
| 1 |
| 2 |
代入t1、t2,解得:v0=
|
落到A点时下落的竖直高度y0=
| 1 |
| 2 |
| x12h |
| (x2-x1)2 |
故B正确,A、C、D错误.
故选B.
点评:解决本题的关键掌握处理平抛运动的方法,平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目

 B.初速度为
B.初速度为 
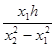 D.竖直高度为
D.竖直高度为 


 B.初速度为
B.初速度为

 D.竖直高度为
D.竖直高度为