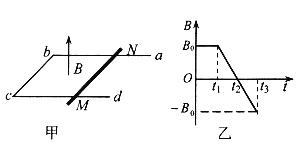题目内容
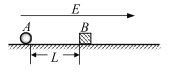
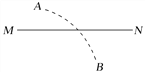
【题目】如图，在水平直角坐标平面xOy内，过原点O沿y轴固定一无限长绝缘通电直导线，电流方向沿+y方向、大小恒为I0，其周围空间磁场的磁感应强度大小B＝kI0/x，k为常数、x为离直导线的垂直距离。OA、OB为沿Ⅰ、Ⅳ象限角平分线方向固定，材料、粗细均相同的两根足够长裸直导轨，两导轨在原点O接触良好，但与通电直导线绝缘。cd为长L、材料和粗细与导轨相同的足够长裸金属杆。现使cd杆从原点O开始垂直Ox轴贴着两导轨向+x方向运动，经t秒运动至坐标x处。在这一过程中，cd杆中电流强度大小恒为I。已知导轨、cd杆单位长度电阻为R0，不计导轨中电流产生的磁场的影响。
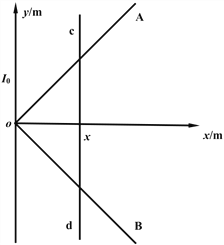
（1）判断cd杆滑动时感应电流的方向，并求t秒末它的速率v与x的关系式；
（2）分析说明cd杆在运动过程中加速度大小的变化情况；
（3）求t秒末cd杆两端电压U与x的关系式；
（4）求t秒内cd杆产生的焦耳热Q与x的关系式。
【答案】（1）
（2）杆的加速增大；（3）U=[(1+
)L-2x]IR0（4）Q=2(
-1)kI0Ix
【解析】（1）由安培定则、右手定则可以判定，cd杆中感应电流方向沿+y方向；
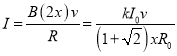
解得： 
（2）由上式，取连续相等两位移Δx，cd杆经过两段位移速度变化量Δv相同，但由于cd杆加速滑动，故后一段位移时间Δt比前一段短，由
，可知杆的加速增大；
（3）t秒末，cd杆在两导轨之间的一段两端电压： 
；
杆伸出导轨外部分两端电压： 
所以cd杆两端电压： 
（4）cd杆受到的安培力： 
cd杆在t秒内，克服安培力的功等于闭合回路中产生的总焦耳热：
练习册系列答案
金钥匙试卷系列答案
相关题目
