题目内容
2008年12月,天文学家通过观测的数据确认了银河系中央的黑洞“人马座A*”的质量与太阳质量的关系.研究发现,有一星体S2绕“人马座A*”做椭圆运动,其轨道半长轴为9.50×102个天文单位(地球公转轨道的半径为一个天文单位),“人马座A*”就处在该椭圆的一个焦点上.观测得到S2星的运行周期为15.2年.(计算结果保留一位有效数字)
(1)已知太阳质量Ms=2.0×1030kg,若将S2星的运行轨道视为半径r=9.50×102个天文单位的圆轨道,试估算“人马座A*”的质量MA;
(2)理论计算表明,当物体的速度达第一宇宙速度的
倍时,物体将逃离天体对它的引力,不再绕天体运行.由黑洞理论可知,任何物体即使是光,也不能逃离黑洞.已知G=6.67×10-11N?m2/kg2,c=3.0×108m/s,求黑洞“人马座A*”的最大半径.
(1)已知太阳质量Ms=2.0×1030kg,若将S2星的运行轨道视为半径r=9.50×102个天文单位的圆轨道,试估算“人马座A*”的质量MA;
(2)理论计算表明,当物体的速度达第一宇宙速度的
| 2 |
分析:(1)研究S2星绕人马座A*做圆周运动,根据万有引力提供向心力,列出等式求出人马座A*的质量.
(2)根据题意得到人马座A*的第一宇宙速度为
,然后根据万有引力提供向心力得到半径.
(2)根据题意得到人马座A*的第一宇宙速度为
| c | ||
|
解答:解:(1)地球绕太阳运行时,万有引力提供向心力,有:
G
=m(
)2r地 ①
同理S2星绕“人马座A*”运行时
G
=m(
)2rS ②
解得:MA=
MS=7×1036kg ③
(2)物体绕“人马座A*”运行时
G
=m
④
解得:v=
由于r增大时,环绕速度变小,故半径最大时,环绕速度最小,由题意可知,“人马座A*”成为黑洞的条件是其环绕速度
v=
⑤
解得:Rm=2G
=1×1010m
答:(1)“人马座A*”的质量为7×1036kg;
(2)黑洞“人马座A*”的最大半径为1×1010m.
G
| mM太 | ||
|
| 2π |
| T地 |
同理S2星绕“人马座A*”运行时
G
| mMA | ||
|
| 2π |
| TS |
解得:MA=
| ||||
|
(2)物体绕“人马座A*”运行时
G
| mMA |
| r2 |
| v2 |
| r |
解得:v=
|
由于r增大时,环绕速度变小,故半径最大时,环绕速度最小,由题意可知,“人马座A*”成为黑洞的条件是其环绕速度
v=
| c | ||
|
解得:Rm=2G
| MA |
| c2 |
答:(1)“人马座A*”的质量为7×1036kg;
(2)黑洞“人马座A*”的最大半径为1×1010m.
点评:本题关键是读懂题意,然后多次根据万有引力提供向心力列式,同时根据题意得到第一宇宙速度大小,最后联立求解,较难.

练习册系列答案
相关题目
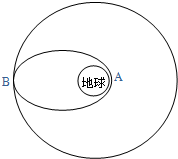 2008年9月25日21时10分,神舟七号飞船成功发射,共飞行2天20小时27分钟,绕地球飞行45圈后,于9月28日17时37分安全着陆.航天员翟志刚着“飞天”舱外航天服,在刘伯明的配合下,成功完成了空间出舱活动,进行了太空行走.出舱活动结束后,释放了伴飞卫星,并围绕轨道舱进行伴飞实验.神舟七号是由长征-2F运载火箭将其送入近地点为A,远地点为B的椭圆轨道上,实施变轨后,进入预定圆轨道,其简化的模拟轨道如图12所示.假设近地点A距地面高度为h,飞船在预定圆轨道上飞行n圈所用的时间为t,地球表面的重力加速度为g,地球半径R,试求:
2008年9月25日21时10分,神舟七号飞船成功发射,共飞行2天20小时27分钟,绕地球飞行45圈后,于9月28日17时37分安全着陆.航天员翟志刚着“飞天”舱外航天服,在刘伯明的配合下,成功完成了空间出舱活动,进行了太空行走.出舱活动结束后,释放了伴飞卫星,并围绕轨道舱进行伴飞实验.神舟七号是由长征-2F运载火箭将其送入近地点为A,远地点为B的椭圆轨道上,实施变轨后,进入预定圆轨道,其简化的模拟轨道如图12所示.假设近地点A距地面高度为h,飞船在预定圆轨道上飞行n圈所用的时间为t,地球表面的重力加速度为g,地球半径R,试求: