题目内容
 如图所示,一台模型发电机的电枢是矩形导线框abcd,其ab和cd边长为L1=0.4m,ad和bc边长L2=0.2m,匝数为n=100,它在磁感应强度B=0.2T的匀强磁场中绕通过线框对称中心线,且垂直于磁场方向的轴OO’匀速转动,当开关S断开时,电压表的示数为10
如图所示,一台模型发电机的电枢是矩形导线框abcd,其ab和cd边长为L1=0.4m,ad和bc边长L2=0.2m,匝数为n=100,它在磁感应强度B=0.2T的匀强磁场中绕通过线框对称中心线,且垂直于磁场方向的轴OO’匀速转动,当开关S断开时,电压表的示数为10| 2 |
(2)S闭合后,当导线框从图示位置转过θ=600过程中通过灯泡的电荷量.(计算结果保留二位有效数字)
分析:(1)根据电压表有效值,可求出最大值,由Em=NBSω 即可求解;
(2)根据灯泡的额定电压与额定功率,与闭合电路欧姆定律及法拉第电磁感应定律,即可求解.
(2)根据灯泡的额定电压与额定功率,与闭合电路欧姆定律及法拉第电磁感应定律,即可求解.
解答:解:(1)当S断开,电压表示数为1O
V,则:
Em=
×1O
V=20V ①
而Em=NBSω ②
由①②式可得:ω=12.5(rad/s) ③
(2)S闭合,“10V 1OW”灯泡正常发光,则电路中电流:
I=
④
而E=I(R+r)⑤
线框转过θ=600过程中通过灯泡的电荷量:Q=
△t ⑥
而
=
⑦
又
=
=
⑧
则通过灯光的电量q=
代入数据,解得:q=0.08C
答:(1)导线框abcd在磁场中转动的角速度12.5(rad/s);
(2)S闭合后,当导线框从图示位置转过θ=600过程中通过灯泡的电荷量0.08C.
| 2 |
Em=
| 2 |
| 2 |
而Em=NBSω ②
由①②式可得:ω=12.5(rad/s) ③
(2)S闭合,“10V 1OW”灯泡正常发光,则电路中电流:
I=
| P |
| U |
而E=I(R+r)⑤
线框转过θ=600过程中通过灯泡的电荷量:Q=
. |
| I |
而
. |
| I |
| ||
| (R+r) |
又
. |
| E |
| △? |
| △t |
| NBS(1-cos60°) |
| △t |
则通过灯光的电量q=
| NBS(1-cos60°) |
| R+r |
代入数据,解得:q=0.08C
答:(1)导线框abcd在磁场中转动的角速度12.5(rad/s);
(2)S闭合后,当导线框从图示位置转过θ=600过程中通过灯泡的电荷量0.08C.
点评:考查交流电的有效值与最大值的关系,掌握最大值Em=NBSω 公式,理解闭合电路欧姆定律与法拉第电磁感应定律的应用.

练习册系列答案
相关题目
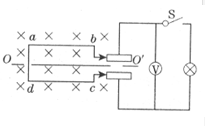
 V.开关S闭合时,外电路上标有“lO V 10W”的灯泡恰好正常发光.求:(1)导线框abcd在磁场中转动的角速度?
V.开关S闭合时,外电路上标有“lO V 10W”的灯泡恰好正常发光.求:(1)导线框abcd在磁场中转动的角速度?

 这台发电机的内阻为多少?
这台发电机的内阻为多少?