题目内容
在某行星表面附近自高h处以初速度v水平抛出的小球,水平射程可达x,已知该行星的半径为R,如果在该行星上发射一颗人造卫星,则它在该行星表面附近做匀速圆周运动的周期T是多少?
【答案】分析:根据平抛运动的高度、初速度和水平射程求出重力加速度.人造卫星在该行星表面附近做匀速圆周运动时,由重力提供向心力,由牛顿第二定律求出周期.
解答:解:小球在行星表面附近做平抛运动时,竖直方向做自由落体运动,则有
h=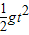 ①
①
水平方向做匀速直线运动,则有
x=vt ②
由①②得,g=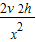 ③
③
人造卫星在该行星表面附近做匀速圆周运动时,由重力提供向心力,由牛顿第二定律得
mg=
得,T= ④
④
将③代入④得,T=
答:人造卫星在该行星表面附近做匀速圆周运动的周期T= .
.
点评:本题是万有引力与平抛运动的综合,其桥梁是重力加速度.对于卫星问题,基本思路是:由万有引力提供向心力,列方程求解周期、线速度等物理量.
解答:解:小球在行星表面附近做平抛运动时,竖直方向做自由落体运动,则有
h=
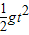 ①
①水平方向做匀速直线运动,则有
x=vt ②
由①②得,g=
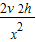 ③
③人造卫星在该行星表面附近做匀速圆周运动时,由重力提供向心力,由牛顿第二定律得
mg=

得,T=
 ④
④将③代入④得,T=

答:人造卫星在该行星表面附近做匀速圆周运动的周期T=
 .
.点评:本题是万有引力与平抛运动的综合,其桥梁是重力加速度.对于卫星问题,基本思路是:由万有引力提供向心力,列方程求解周期、线速度等物理量.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目