题目内容
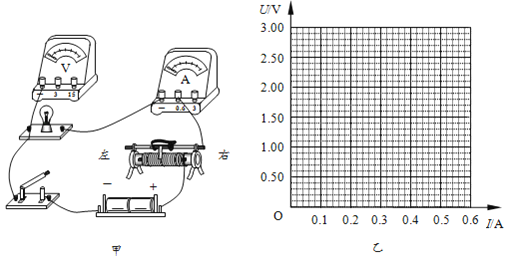
【题目】如图,质量为m的A球下面固定一轻质弹簧,用长度为l的轻绳穿过弹簧连接在B球上,弹簧原长远小于轻绳长度(绳未连接在弹簧上),B球离地面的高度也为1;手拿A球,A球与B球处于静止状态,将A球由静止释放,B球与地面每次碰撞时反弹速度前速度的一半,B球第一次触地反弹后在空中与A球发生碰撞,碰撞后瞬间弹簧被用缩到最短,此时弹簧锁定。然后A球与B球一起下落,B球第二次触地反弹后的瞬间,弹簧解除锁定,同时轻绳断裂,A球被弹起。整个过程A、B球都保持竖直方向,且A球一直在上,B球在下,所有碰时间均不计。(重力加速度为g,最后结果可以用根号表示)
(1)B球第一次触地后到B球与A球碰撞的时间;
(2)要求B球与A球碰撞后瞬间弹簧被压缩到最短时弹簧的势能达到最大,求B球的质量M满足的条件和弹簧势能的最大值Ep;
(3)在B球的质量M满足(2)问的条件下,求B球第二次触地反弹后A球被弹起的最大高度。

【答案】(1)![]() (2)M=8m;2mgl(3)12.5l
(2)M=8m;2mgl(3)12.5l
【解析】
(1)B球第一次触地时的速度
![]()
此时A的速度也为
![]()
B球反弹的速度
![]()
则两球第一次相遇时:
![]()
解得
![]()
(2)两球相遇时的速度
![]()
![]()
当弹簧压缩到最短时,两球共速,设向上为正方向,由动量守恒定律
![]()
当弹簧的弹性势能最大时,则v=0,解得:
M=8m
此时弹簧的最大弹性势能:
![]()
(3)两球第一次相遇 时离地面的高度:
![]()
则第二次落地的速度
![]()
此时两球反弹速度为
![]()
此时解除锁定后,弹簧的弹性势能转化为AB的动能,则由能量关系:
![]()
由动量守恒:
![]()
解得
![]()
A上升的高度:
![]()
解得
![]()

练习册系列答案
相关题目