题目内容
（A选做） 宇航员登上某一星球并在该星球表面做实验，用一根不可伸缩的轻绳跨过轻质定滑轮，一端挂一吊椅，另一端被坐在吊椅上的宇航员拉住，如图所示．宇航员的质量m1=65kg，吊椅的质量m2=15kg，当宇航员与吊椅以a=1m/s2的加速度匀加速上升时，宇航员对吊椅的压力为l75N．（忽略定滑轮摩擦）（1）求该星球表面的重力加速度g；
（2）若该星球的半径6×105，地球半径6×106，地球表面的重力加速度10m/s2，求该星球的平均密度与地球的平均密度之比．
分析：（1）对整体以及隔离对宇航员受力分析，根据牛顿第二定律求出重力加速度的大小．
（2）根据密度公式以及万有引力等于重力这一理论，求出星球的平均密度和地球的平均密度之比．
（2）根据密度公式以及万有引力等于重力这一理论，求出星球的平均密度和地球的平均密度之比．
解答：解：（1）设宇航员受到绳向上的拉力为F，由于跨过定滑轮的两段绳子拉力相等，吊椅受到绳的拉力也是F，对他和吊椅整体进行受力分析如图所示，则有：
2F-（m1+m2）g=（m1+m2）a
设吊椅对宇航员的支持力为FN，压力为FN′，根据牛顿第三定律得：FN=FN′．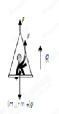
对宇航员，由牛顿第二定律得，F+FN-m1g=m1a
代入数据解得g=6m/s2．
（2）由星球密度ρ=
和
=m′g得，
该星球的平均密度与地球的平均密度之比
=
，
代入数值解得
=
=0.64．
答：（1）星球表面的重力加速度为6m/s2．
（2）该星球的平均密度与地球的平均密度之比0.64．
2F-（m1+m2）g=（m1+m2）a
设吊椅对宇航员的支持力为FN，压力为FN′，根据牛顿第三定律得：FN=FN′．
对宇航员，由牛顿第二定律得，F+FN-m1g=m1a
代入数据解得g=6m/s2．
（2）由星球密度ρ=
| M | ||
|
| GMm′ |
| R2 |
该星球的平均密度与地球的平均密度之比
| ρ |
| ρ0 |
| gR0 |
| g0R |
代入数值解得
| ρ |
| ρ0 |
| 16 |
| 25 |
答：（1）星球表面的重力加速度为6m/s2．
（2）该星球的平均密度与地球的平均密度之比0.64．
点评：解决本题的关键能够正确地受力分析，运用牛顿第二定律进行求解，注意整体法和隔离法的运用．
练习册系列答案
相关题目
2003年10月15日9时整，中国第一艘载人飞船“神舟五号”由“长征2号F”运载火箭从甘肃酒泉卫星发射中心发射升空，10分钟后，成功进入预定轨道，中国首位航天员杨利伟，带着中国人的千年企盼梦圆浩瀚太空，中国成为世界上第三个能够独立开展载人航天活动的国家．
(1)火箭在加速上升过程中宇航员处于________状态(选填“超重”或“失重”)．由于地球在自西向东不停地自转，为节省燃料，火箭在升空后，应向________方向飞行(选填“偏东”、“偏西”)．
(2)目前中国正在实施“嫦娥一号”登月工程，已知月球表面没有空气，没有磁场，引力为地球的
，假如登上月球，你能够________(填代号)
| A．用指南针判断方向 |
| B．轻易跃过3米高度 |
| C．乘坐热气球探险 |
| D．做托里拆利实验时发现内外水银面高度差为76cm |
