题目内容
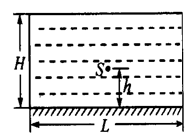
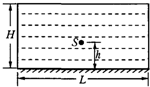 如图所示的圆柱形容器中盛满折射率n=2的某种透明液体,容器底部安装一块平面镜,容器直径L=2H,在圆心正上方高度h处有一点光源S,要使人从液体表面上任意位置处能够观察到点光源S发出的光,h应该满足什么条件?
如图所示的圆柱形容器中盛满折射率n=2的某种透明液体,容器底部安装一块平面镜,容器直径L=2H,在圆心正上方高度h处有一点光源S,要使人从液体表面上任意位置处能够观察到点光源S发出的光,h应该满足什么条件?分析:要使人从液体表面上任意位置处能够观察到点光源S发出的光,点光源发出的光必须全部能折射进入空气中,根据对称性,作出点光源经平面镜所成的像.当光射向水面时,入射角应不大于临界角,光线才能射入空气中.由几何知识求出h应满足的条件.
解答: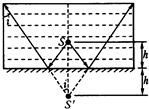 解:点光源S通过平面镜所成像为S',如图所示,要使人从液体表面上任意位置处能够观察到点光源S发出的光,即相当于像S'发出的光在水面不发生全反射,则:
解:点光源S通过平面镜所成像为S',如图所示,要使人从液体表面上任意位置处能够观察到点光源S发出的光,即相当于像S'发出的光在水面不发生全反射,则:
入射角i≤C,C为全反射临界角,而sinC=
=
,得:C=30°
由几何知识得,tani=
≤tanC,L=2H,
得到:h≥(
-1)H,
所以:H>h≥(
-1)H.
答:要使人从液体表面上任意位置处能够观察到点光源S发出的光,h应该满足的条件是:H>h≥(
-1)H
 解:点光源S通过平面镜所成像为S',如图所示,要使人从液体表面上任意位置处能够观察到点光源S发出的光,即相当于像S'发出的光在水面不发生全反射,则:
解:点光源S通过平面镜所成像为S',如图所示,要使人从液体表面上任意位置处能够观察到点光源S发出的光,即相当于像S'发出的光在水面不发生全反射,则:入射角i≤C,C为全反射临界角,而sinC=
| 1 |
| n |
| 1 |
| 2 |
由几何知识得,tani=
| ||
| H+h |
得到:h≥(
| 3 |
所以:H>h≥(
| 3 |
答:要使人从液体表面上任意位置处能够观察到点光源S发出的光,h应该满足的条件是:H>h≥(
| 3 |
点评:本题要利用对称性作出平面镜所成的像,点光源发出的光好像从虚像发出的.再根据临界角和几何知识求解h满足的条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2007?盐城一模)选修3-3试题:
(2007?盐城一模)选修3-3试题: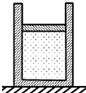 如图所示的圆柱形容器内用活塞密封一定质量的理想气体,容器横截面积为S,活塞质量为m,大气压强为p0,重力加速度为g,活塞处于静止状态.现对容器缓缓加热使容器内的气体温度升高t℃,活塞无摩擦地缓慢向上移动了h,在此过程中气体吸收的热量为Q,问:
如图所示的圆柱形容器内用活塞密封一定质量的理想气体,容器横截面积为S,活塞质量为m,大气压强为p0,重力加速度为g,活塞处于静止状态.现对容器缓缓加热使容器内的气体温度升高t℃,活塞无摩擦地缓慢向上移动了h,在此过程中气体吸收的热量为Q,问: 如图所示的圆柱形容器内用活塞密封一定质量的气体,已知容器横截面积为S,活塞重为G,大气压强为P0.若活塞固定,密封气体温度升高1℃,需吸收的热量为Q1;若活塞不固定而能无摩擦滑动,仍使密封气体温度升高1℃,需吸收的热量为Q2.求在活塞可自由滑动时,密封气体温度升高l℃,活塞上升的高度h.
如图所示的圆柱形容器内用活塞密封一定质量的气体,已知容器横截面积为S,活塞重为G,大气压强为P0.若活塞固定,密封气体温度升高1℃,需吸收的热量为Q1;若活塞不固定而能无摩擦滑动,仍使密封气体温度升高1℃,需吸收的热量为Q2.求在活塞可自由滑动时,密封气体温度升高l℃,活塞上升的高度h.