Question

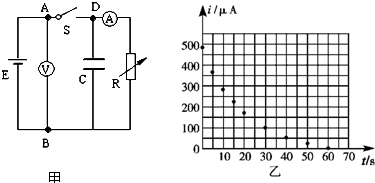
如图甲所示是一种测量电容的实验电路图，实验是通过对高阻值电阻放电的方法，测出电容器充电至其两端电压为U时所带电量Q，从而再求出电容器的电容C.某同学在一次实验时的情况如下：接通开关S，调节电阻箱R的阻值，使小量程电流表的指针偏转近满刻度，记下此时电流表的示数是I₀＝490 μA，电压表的示数U₀＝6.0 V，I₀、U₀分别是电容器放电时的初始电压和电流．断开开关S，同时开始计时，每隔5 s(10 s)测读一次电流I的值，将测得数据填入如下所示的表格中．

(1)在图乙坐标系上画出I－t图线；

(2)图乙中图线与坐标轴所围成面积的物理意义是_______________________________．

(3)该电容器的电容为：_______________ ________________________________.

电流I/μA	490	380	280	230	180	100	50	25	10
时间t/s	0	5	10	15	20	30	40	50	55

Answer 1

解析　(1)根据实验所记录的数据在坐标纸中作I－t图像(如图丙所示)，注意作图时要描点作图，然后用平滑的曲线连接；(2)由电流强度的定义式q＝It和在坐标纸中作出的I－t图线与运动学中的v－t图线类比可知，I－t图线与时间轴所围成的面积表示放电过程中通过回路的总电量；(3)I－t图线与时间轴所围成的方格数为34个，则算出放电过程中通过回路的总电量为q＝34×50×10^－6×5 C＝8.5×10^{－3 C(32}～36个均可)，由电容定义式可知C＝＝F＝1.42×10^－3F(1.33×10^－3～1.50×10^－3均正确)．

答案　(1)见解析　(2)放电量　(3)1.42×10^－3 F