题目内容
如图所示,有一内壁光滑的闭合椭圆形管道,置于竖直平面内,MN是通过椭圆中心O点的水平线。已知一小球从M点出发,初速率为v0,沿管道MPN运动,到N点的速率为v1,所需时间为t1;若该小球仍由M点以出速率v0出发,而沿管道MQN运动,到N点的速率为v2,所需时间为t2。则( )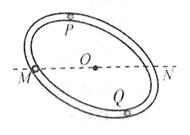
| A.v1=v2,t1>t2 | B.v1<v2,t1>t2 | C.v1=v2,t1<t2 | D.v1<v2,t1<t2 |
A
解析试题分析:小球在运动过程中机械能守恒,故两次到达N点的速度大小相同,且均等于初速度,即v1=v2=v0;两小球的运动过程分别为先加速后减速和先减速后加速,定性做出小球运动的速率—时间图象如下图:
则图线与坐标轴所围成的面积表示小球的运动路程,小球两次的路程相等,故两次图线与坐标轴所围面积相同,由图可知,t1>t2,A正确。
考点:机械能守恒定律、运动的图象

 名师点拨卷系列答案
名师点拨卷系列答案将小球a从地面以初速度v0竖直上抛的同时,将另一相同质量的小球b从距地面高h处以初速度v0水平抛出,两球恰在处相遇(不计空气阻力,取地面为零势能面)。则下列说法正确的是
| A.两球同时落地 |
| B.相遇时两球速度大小相等 |
| C.从开始运动到相遇,球a动能的减少量等于球b动能的增加量 |
| D.相遇后到落地前的任意时刻,球a的机械能小于球b的机械能 |
(单选)如图甲所示,绷紧的水平传送带始终以恒定速率v1运行.初速度大小为v2的小物块从与传送带等高的光滑水平地面上的A处滑上传送带.若从小物块滑上传送带开始计时,小物块在传送带上运动的v-t图象(以地面为参考系)如图乙所示.已知v2>v1,则( )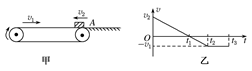
| A.t2时刻,小物块离A处的距离达到最大 |
| B.t2时刻,小物块相对传送带滑动的距离达到最大 |
| C.0~t2时间内,小物块受到的摩擦力方向先向右后向左 |
| D.0~t3时间内,小物块始终受到大小不变的摩擦力作用 |
甲、乙两个质点同时向同一方向做直线运动,它们的v-t图象如图所示,则: ( )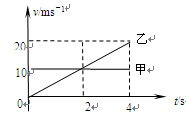
| A.乙比甲运动得快 |
| B.在4s末乙追上甲 |
| C.4s内甲的平均速度等于乙的平均速度 |
| D.乙追上甲时距出发点80m |
如图所示的位移—时间和速度—时间图象中,给出的四条曲线1、2、3、4代表四个不同物体的运动情况。下列描述中正确的是( )
| A.图线1表示物体做曲线运动 |
B. 图象中 图象中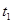 时刻 时刻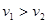 |
C.两图象中,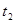 、 、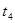 时刻分别表示反向运动 时刻分别表示反向运动 |
D.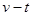 图象中0至 图象中0至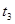 时间内3和4的平均速度大小相等 时间内3和4的平均速度大小相等 |
质点做直线运动的速度—时间图象如图所示,该质点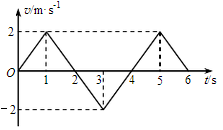
| A.在第1秒末速度方向发生了改变 |
| B.在第2秒末加速度方向发生了改变 |
| C.在前2秒内发生的位移为零 |
| D.第3秒和第5秒末的位置相同 |
斜面上的物体受到平行于斜面向下的力F作用,力F随时间变化的图象及物体运动的速度随时间变化的图象如图所示。由图象中的信息能够求出的物理量或可以确定的关系有(斜面的倾角用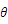 表示)
表示)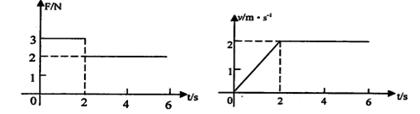
| A.物体的质量m | B.斜面的倾角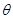 |
C.物体与斜面间的动摩擦因数 | D.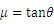 |
如图所示,一个物体的运动速度时间图像如图所示,其中t1-t2时间段为曲线,其它时间段为直线,则有关物体的运动,下列说法正确的是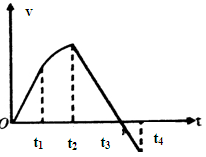
| A.0<t<t1时间段各个时刻的加速度一定大于t1<t<t2时间段各个时刻的加速度 |
| B.t2时刻物体的速度方向发生变化 |
| C.t2时刻物体的位移开始减小 |
| D.t2时刻物体的速度方向未发生变化 |
一位同学乘坐电梯从六楼下到一楼的过程中,其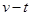 图象如图所示.下列说法正确的是( )
图象如图所示.下列说法正确的是( )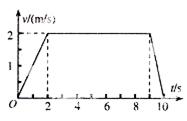
| A.前2s内该同学处于超重状态 |
| B.前2s内该同学的加速度是最后1s内的2倍 |
| C.该同学在10s内的平均速度是1m/s |
| D.该同学在10s内通过的位移是17m |