题目内容
【题目】如图所示，
为半径
的
光滑圆弧轨道，下端
恰好与小车右端平滑对接，小车质量
，车长
，现有一质量
的滑块，由轨道顶端无初速释放，滑到端后冲上小车，已知地面光滑，滑块与小车上表面间的动摩擦因数
，当车运行了
时，车被地面装置锁定。（
）。求：
(1)滑块刚到达端瞬间，轨道对它支持力的大小；
(2)车被锁定时，车右端距轨道端的距离；
(3)从车开始运动到被锁定的过程中，滑块与车面间由于摩擦而产生的内能大小。
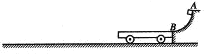
【答案】(1)30N；(2)1m；(3)6J
【解析】
(1)滑块从光滑圆弧轨道过程，只有重力做功，机械能守恒。经过
端时由重力和轨道的支持力的合力提供向心力，根据机械能守恒定律和牛顿第二定律求解轨道的支持力。
(2)根据牛顿第二定律分别求出滑块滑上小车后滑块和小车的加速度，由速度公式求出两者速度所经历的时间，再求解车被锁定时，车右端距轨道端的距离；
(3)从车开始运动到被锁定的过程中，系统损失的机械能转化为内能，求出滑块相对于小车滑动的距离，根据能量守恒定律求出内能。
(1)滑块从光滑圆弧轨道过程，根据机械能守恒定律得
解得
滑块经过端时，由牛顿第二定律得
解得
(2)当滑块滑上小车后，由牛顿第二定律，对滑块有
解得
对小车有
解得
设经时间
两者达到共同速度，则有
联立解得
由于
，此时小车还未被锁定，两者的共同速度
两者以共同速度运动时间为
故车被锁定时，车右端距轨道端的距离
(3)从车开始运动到被锁定的过程中，滑块相对小车滑动的距离
所以系统损失的机械能即产生的内能为
练习册系列答案
相关题目
