题目内容
2.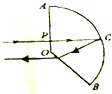 如图所示,空气中有一块截面为扇形的玻璃砖,折射率为$\sqrt{3}$,现有一细光束,垂直射到AO面上,经玻璃砖反射、折射后,经OB面平行于入射光束射出,∠AOB为120°,圆半径为R,则入射点P距圆心O的距离为( )
如图所示,空气中有一块截面为扇形的玻璃砖,折射率为$\sqrt{3}$,现有一细光束,垂直射到AO面上,经玻璃砖反射、折射后,经OB面平行于入射光束射出,∠AOB为120°,圆半径为R,则入射点P距圆心O的距离为( )| A. | $\frac{\sqrt{6}-\sqrt{2}}{4}$R | B. | $\frac{\sqrt{2}+\sqrt{3}}{2}$R | C. | $\frac{R}{2}$ | D. | $\frac{\sqrt{3}}{2}$R |
分析 作出光路图,由几何知识得到光线从OB射出时的折射角,由折射定律求出光线在OB面的入射角,根据几何知识求出∠PCQ,由反射光路的对称性,得到∠PCO,再求解入射点P距圆心O的距离OP.
解答 解:由图可知,光线从OB射出时的折射角为60°,设光线在OB面的入射角为α.
由折射定律得$\frac{sin60°}{sinα}=\sqrt{3}$,
则α=30°,即光在OB面的入射角为30°,所以∠CQB=60°
由几何关系可知,∠PCQ=360°-90°-(90°+30°)-120°=30°,
连接OC,根据对称性得知∠PCO=15°,所以OP=Rsin15°=$\frac{\sqrt{6}-\sqrt{2}}{4}$R,故A正确.
故选:A.
点评 此题考查光的反射和折射,主要问题是运用几何知识分析角度关系,求出折射角和入射角.

练习册系列答案
相关题目
13.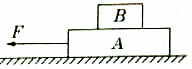 如图所示,A、B两物体在拉力F作用下一起以相同的速度沿F方向匀速运动,关于B物体所受的摩擦力,下列说法正确的是( )
如图所示,A、B两物体在拉力F作用下一起以相同的速度沿F方向匀速运动,关于B物体所受的摩擦力,下列说法正确的是( )
 如图所示,A、B两物体在拉力F作用下一起以相同的速度沿F方向匀速运动,关于B物体所受的摩擦力,下列说法正确的是( )
如图所示,A、B两物体在拉力F作用下一起以相同的速度沿F方向匀速运动,关于B物体所受的摩擦力,下列说法正确的是( )| A. | B物体不受静摩擦力作用 | |
| B. | B物体受到静摩擦力,且方向与F方向相反 | |
| C. | B物体受到A物体对它的静摩擦力,且方向与F方向相同 | |
| D. | B物体受到A物体对它的静摩擦力,且方向与F方向相反 |
10.两束平行的光斜射到平行玻璃砖,经玻璃砖折射后如图所示,则关于这两束光的说法中正确的是( )

| A. | A光的折射率比B光的折射率小 | |
| B. | A光在水中的传播速度比B光在水中的传播速度小 | |
| C. | 从玻璃砖下表面射出的两束光可能不平行 | |
| D. | 若分别将这两束光用同一装置做双缝干涉实验,则A光在光屏上形成的条纹间距大 |
17.如图所示的光学现象中,下列的描述或解释错误的是( )


| A. | 图(a)中,小孔成的像是倒立的实像,反映了光在同种介质中沿直线传播 | |
| B. | 图(b)中,人配戴的凹透镜可以矫正近视眼,利用了光的折射原理 | |
| C. | 图(c)中,白光通过三棱镜可以分解成多种色光,是因为不同颜色的光通过玻璃时偏 折的角度不同 | |
| D. | 图(d)中,因漫反射的反射光线杂乱无章,因此有的光线可能不遵循光的反射定律 |
7. 如图所示,等腰三棱镜的顶角为30°,光线垂直棱镜的一个腰射入棱镜,从另一个腰射出,出射光线偏离原来光线方向15°角,则该棱镜材料的折射率是( )
如图所示,等腰三棱镜的顶角为30°,光线垂直棱镜的一个腰射入棱镜,从另一个腰射出,出射光线偏离原来光线方向15°角,则该棱镜材料的折射率是( )
 如图所示,等腰三棱镜的顶角为30°,光线垂直棱镜的一个腰射入棱镜,从另一个腰射出,出射光线偏离原来光线方向15°角,则该棱镜材料的折射率是( )
如图所示,等腰三棱镜的顶角为30°,光线垂直棱镜的一个腰射入棱镜,从另一个腰射出,出射光线偏离原来光线方向15°角,则该棱镜材料的折射率是( )| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 2 | D. | $\sqrt{3}$ |
11.一个接在交流电路中的理想变压器,它的初级线圈和次级线圈一定具有相同数值的物理量是( )
| A. | 电流强度 | B. | 电压 | C. | 交流电频率 | D. | 磁通量 |
12.比较α、β、γ三种射线的电离作用和穿透能力( )
| A. | β射线的电离作用最强 | B. | γ射线的电离作用最强 | ||
| C. | α射线的穿透能力最强 | D. | γ射线的穿透能力最强 |