题目内容
【题目】一根长为l的丝线吊着一质量为m,带电荷量为q的小球静止在水平向右的匀强电场中,如图所示,丝线与竖直方向成37°角,先突然将该电场方向变为向下且大小不变,不考虑因电场的改变而带来的其它影响(重力加速度为g,sin37°=0.6,cos37°=0.8)求:
(1)匀强电场的电场强度的大小
(2)求小球经过最低点时丝线的拉力大小.
【答案】
(1)解:小球静止在电场中受力如下图所示,显然小球带正电,由平衡条件得:
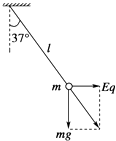
mgtan37°=qE…①
故有:E= ![]() …②
…②
答:匀强电场的电场强度的大小为 ![]() ;
;
(2)解:电场方向变成向下后,小球开始摆动做圆周运动,重力、电场力对小球做正功.由动能定理得:
![]() mv2=(mg+qE)l(1﹣cos37°)…③
mv2=(mg+qE)l(1﹣cos37°)…③
由圆周运动知识,在最低点时,小球受力情况如下图所示,由牛顿第二定律有:
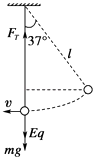
FT﹣(mg+qE)=m ![]() …④
…④
由③④解得:FT= ![]() mg.
mg.
答:小球经过最低点时丝线的拉力为 ![]() mg.
mg.
【解析】(1)对小球受力分析正交分解进而求出电场强度。
(2)在复合场中先求最低点的速度,再根据向心力的公式求出拉力大小。

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目