题目内容
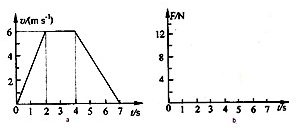
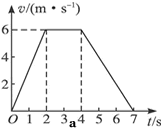
图a为一电梯上升过程中的v-t图象，若电梯地板上放一质量为1kg的物体，g取10m/s2．（1）求电梯前2s内和后3s内的加速度大小；
（2）求2-4s内物体对地板的压力大小；
（3）在图b中画出电梯上升过程中地板对物体的支持力F随时间变化的图象．
【答案】分析：（1）根据速度时间图线的斜率求出匀加速运动和匀减速运动的加速度大小．
（2）在2-4s内，电梯做匀速直线运动，物体处于平衡状态，重力与支持力平衡，根据牛顿第三定律，支持力与压力相等．
（3）根据牛顿第二定律分别求出匀加速运动和匀减速运动阶段的支持力，然后作出F与时间t的图线．
解答：
解：（1）前2s内加速度的大小a1=
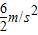=3m/s2，
后3s内加速度的大小a2=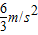
=2m/s2．
（2）2s-4s内电梯匀速上升，由平衡条件可得，N=mg=10N
根据牛顿第三定律得，物体对地板的压为FN=N=10N．
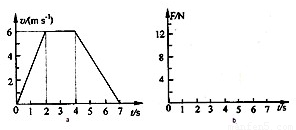
（3）0-2内电梯加速上升，由牛顿第二定律得F-mg=ma1，解得F=13N；
2s-4s内F=FN=10N；
4s-6s内电梯减速上升，由牛顿第二定律得mg-F=ma2，解得F=8N．
所以电梯上升过程中地板对物体的支持力F随时间t变化的图象如图所示
点评：解决本题的关键知道速度-时间图线的斜率表示加速度，会根据牛顿第二定律求出匀加速运动和匀减速运动的支持力大小．
（2）在2-4s内，电梯做匀速直线运动，物体处于平衡状态，重力与支持力平衡，根据牛顿第三定律，支持力与压力相等．
（3）根据牛顿第二定律分别求出匀加速运动和匀减速运动阶段的支持力，然后作出F与时间t的图线．
解答：
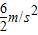解：（1）前2s内加速度的大小a1==3m/s2，后3s内加速度的大小a2=
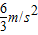=2m/s2．（2）2s-4s内电梯匀速上升，由平衡条件可得，N=mg=10N
根据牛顿第三定律得，物体对地板的压为FN=N=10N．
（3）0-2内电梯加速上升，由牛顿第二定律得F-mg=ma1，解得F=13N；
2s-4s内F=FN=10N；
4s-6s内电梯减速上升，由牛顿第二定律得mg-F=ma2，解得F=8N．
所以电梯上升过程中地板对物体的支持力F随时间t变化的图象如图所示
点评：解决本题的关键知道速度-时间图线的斜率表示加速度，会根据牛顿第二定律求出匀加速运动和匀减速运动的支持力大小．
练习册系列答案
名校课堂系列答案
相关题目
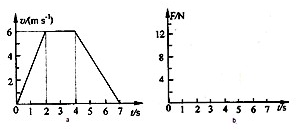图a为一电梯上升过程中的v-t图象，若电梯地板上放一质量为1kg的物体，g取10m/s2．
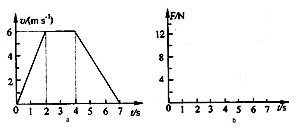图a为一电梯上升过程中的v-t图象，若电梯地板上放一质量为1kg的物体，g取10m/s2．
