题目内容
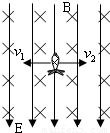
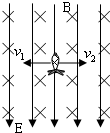在一次实战训练中，有一炮弹被从地面竖直向上射出，当炮弹到达最高点时突然炸裂为两块，其质量分别为m1=1kg、m2=0.8kg，且在炸裂过程中分别带上q=0.2C等量异种电荷，其中m1带负电．设在炸裂处，有一水平宽度L=20m1的正交匀强电、磁场，如图所示．匀强磁场B=0.1T，方向垂直纸面向里，匀强电场方向竖直向下．设炸裂时，炮弹正处在正交电磁场中心，炸裂后，m1在正交电、磁场中向左做直线运动，m2在正交电磁场中向右做直线运动．（g=10m/s2）求：（1）电场强度的大小？
（2）爆炸对m1、m2做的功各为多少？
分析：（1）根据两部分炸弹分别做匀速直线运动，根据平衡以及动量守恒定律求出两物体的速度以及电场强度的大小和方向．
（2）根据动能定理列出等式求解．
（2）根据动能定理列出等式求解．
解答：解：（1）由动量守恒定律得：m1v1-m2v2=0…①
带电物体在洛仑兹力作用下的直线运动是匀速直线运动，根据受力有：
Bqv1+Eq=m1g…②
Bqv2-Eq=m2g…③
联立①②③得：
两物体匀速运动的速度
∴v1=
=40m/s
v2=
=50m/s
所加电场为：
E=
=
=10V/m
（3）由动能定理得：爆炸对两物体做的功为：
w1=△E1=
=800J
w2=△E2=
m1
=1000J
答：（1）电场强度的大小是10V/m
（2）爆炸对m1、m2做的功各为800J，1000J．
带电物体在洛仑兹力作用下的直线运动是匀速直线运动，根据受力有：
Bqv1+Eq=m1g…②
Bqv2-Eq=m2g…③
联立①②③得：
两物体匀速运动的速度
∴v1=
| m2g |
| Bq |
v2=
| m1g |
| Bq |
所加电场为：
E=
| m1g-Bqv1 |
| q |
| m1g-m2g |
| q |
（3）由动能定理得：爆炸对两物体做的功为：
w1=△E1=
| 2 1 |
w2=△E2=
| 1 |
| 2 |
| v | 2 2 |
答：（1）电场强度的大小是10V/m
（2）爆炸对m1、m2做的功各为800J，1000J．
点评：解决本题的关键知道爆炸时在水平方向上动量守恒，在电磁场中运动时两炸弹受力平衡，出磁场后做平抛运动．
练习册系列答案
阅读快车系列答案
相关题目
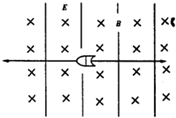在一次实战训练中，有一炮弹被以初速度为v0从地面竖直向上射出．当炮弹到达最高点h=80m处时，突然炸裂为二块，其质量分别为m1=1kg、m2=0.8kg，且在炸裂过程中分别带上了q=0.2C等量异种电荷，其中m1带负电．设在炸裂处，有一水平宽度L=20m的正交匀强电磁场，如图，匀强磁场方向垂直于纸面向里，大小为B=1.0T，匀强电场方向竖直．设炸裂时，炮弹正处在正交电磁场的中心，炸裂后，m1在正交电磁场中向左做直线运动，m2在正交电磁场中向右做直线运动．（g=10m/s2）
