Question

【题目】如图所示，水平传送带长L=12m，且以v=5m/s的恒定速率顺时针转动，光滑曲面与传送带的右端B点平滑连接，有一质量m=2kg的物块从距传送带高h=5m的A点由静止开始滑下。已知物块与传送带之间的滑动摩擦因数μ=0.5，重力加速度g取10m/s2，求：

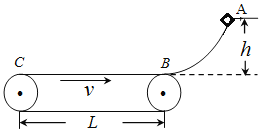
（1）物块距传送带左端C的最小距离；

（2）物块再次经过B点后滑上曲面的最大高度。

Answer 1

【答案】（1）2m（2）1.25m

【解析】（1）物块从A到B的过程中，由机械能守恒列式得：mgh＝mvB2
解得：vB=10m/s
物块在传送带上向左运动的过程中，取水平向左为正方向，通过受力分析后，
由牛顿第二定律得：-μmg=ma得：a=-5m/s2，
由运动学公式得： vB2＝2ax1
解得：

且t1＝＝2s
那么，物块距传送带左端C的最小距离dmin=L-x1=2m
（2）物块在传送带上向右运动的过程中，取水平向右为正方向，通过受力分析后，
由牛顿第二定律得：μmg=ma′得：a′=5m/s
由于传送带的速度v=5m/s由运动学公式v=at2得：t2=1s

＝2.5m＜10m
则物块向右运动经过B点时的速度v=5m/s
那么，物块经过B点后滑上曲面的过程中，由机械能守恒定律得：mghm＝mv2
即：hm=1.25m