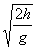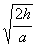题目内容
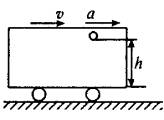
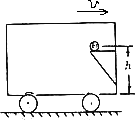
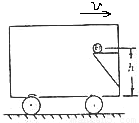
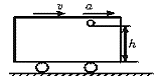
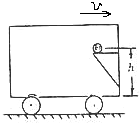 如图所示,正以速度v匀速行驶的车厢,忽然改为以加速度a作匀加速直线运动,则离车厢底为h高的小球将落下,落下点距架子的水平距离为( )
如图所示,正以速度v匀速行驶的车厢,忽然改为以加速度a作匀加速直线运动,则离车厢底为h高的小球将落下,落下点距架子的水平距离为( )分析:小球落下后做的是平抛运动,可以分解为水平和竖直两个方向列方程,求得水平位移;同时车厢是匀加速运动的,车厢在水平方向上也有位移,落点到货架边缘的水平距离是它们水平位移的差.
解答:解:小球做平抛运动,在竖直方向上,小球做自由落体运动.
由h=
gt2
可得运动时间t=
,
在水平方向上,小球做初速度为v0的匀速运动,同时货架做初速度为v0的匀加速运动,
小球在水平方向的位移是S1=v0t,
货架运动距离是 S2=v0t+
at2,
小球的落点到货架边缘的水平距离是
S=S2-S1=v0t+
at2-v0t=
at2=
故选B.
由h=
| 1 |
| 2 |
可得运动时间t=
|
在水平方向上,小球做初速度为v0的匀速运动,同时货架做初速度为v0的匀加速运动,
小球在水平方向的位移是S1=v0t,
货架运动距离是 S2=v0t+
| 1 |
| 2 |
小球的落点到货架边缘的水平距离是
S=S2-S1=v0t+
| 1 |
| 2 |
| 1 |
| 2 |
| ah |
| g |
故选B.
点评:本题考查平抛运动和匀加速运动规律的应用,同时同学们比较容易忽略的是车厢的运动,由于车厢是加速运动的,车厢在水平方向上也有位移,所以不能单单求小球在水平方向的位移.

练习册系列答案
相关题目
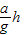
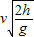
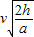
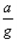 ·h
·h