题目内容
9．
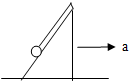将质量m=5kg的小球悬挂在一个三角形劈的光滑斜面上，斜面的倾角θ=53°，当劈以加速度a=9.8m/S2向右做加速运动时，绳对小球的拉力有多大．（g=10m/S2，sin53°=0.8，cos53°=0.6）
分析 由牛顿第二定律求出小球对斜面恰好没有压力时的临界加速度，然后应用牛顿第二定律求出绳子对小球的拉力．
解答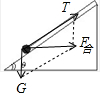 
解：斜面对小球恰好没有支持力时，由牛顿第二定律得：
$\frac{mg}{tan53°}$=ma0，
解得：a0=7.5m/s2，
由于：a=9.8m/s2＞a0=7.5m/s2，
则加速度为9.8m/s2时小球离开斜面，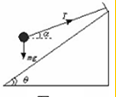
设绳子与水平方向间的夹角为α，
由牛顿第二定律得：
水平方向：Tcosα=ma
竖直方向：Tsinα=mg，
绳子拉力：T=$\sqrt{（ma）^{2}+（mg）^{2}}$≈70N；
答：绳对小球的拉力为70N．
点评 此题最难解决的问题是小球是否飞离了斜面，我们可以用假设法判断出临界加速度来进行比较．
练习册系列答案
相关题目
4．
某学生用电流表和电压表测干电池的电动势和内阻时，所用滑动变阻器的阻值范围为0～20Ω，连接电路的实物图如图所示．该学生接线中错误的和不规范的做法是（ ）
某学生用电流表和电压表测干电池的电动势和内阻时，所用滑动变阻器的阻值范围为0～20Ω，连接电路的实物图如图所示．该学生接线中错误的和不规范的做法是（ ）| A． | 滑动变阻器不起变阻作用 | B． | 电流表接线有错 | ||
| C． | 电压表量程选用不当 | D． | 电压表接线不妥 |
20．
如图所示，斜面上量物块A、B的质量均为m，A、B间用一个细线相连，A、B与斜面间的动摩擦因数分别为μ1，μ2，斜面倾角为θ=37°，它们以a=2m/s2一起匀加速下滑（g=10m/s2），下列说法正确的是（ ）
如图所示，斜面上量物块A、B的质量均为m，A、B间用一个细线相连，A、B与斜面间的动摩擦因数分别为μ1，μ2，斜面倾角为θ=37°，它们以a=2m/s2一起匀加速下滑（g=10m/s2），下列说法正确的是（ ）| A． | 物块B一定受4个力 | B． | μ1≥μ2 | ||
| C． | μ1≤0.5 | D． | μ2≤0.5 |
4．
如图所示，一倾角为α的斜面体置于固定在光滑水平地面上的物体A、B之间，斜面体恰好与物体A、B接触，一质量为m的物体C恰能沿斜面匀速下滑，此时斜面体与A、B间均无作用力，若用平行于斜面的力F沿斜面向下推物体C，在物体C加速下滑过程中，下列说法正确的是（ ）
如图所示，一倾角为α的斜面体置于固定在光滑水平地面上的物体A、B之间，斜面体恰好与物体A、B接触，一质量为m的物体C恰能沿斜面匀速下滑，此时斜面体与A、B间均无作用力，若用平行于斜面的力F沿斜面向下推物体C，在物体C加速下滑过程中，下列说法正确的是（ ）| A． | 物体C与斜面间的动摩擦因数为cotα | |
| B． | 物体C的加速度大小为$\frac{F}{m}$ | |
| C． | 斜面体对物体A有弹力 | |
| D． | 斜面体对物体B有弹力 |
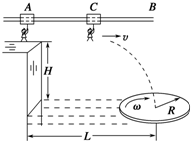某电视台“快乐向前冲”节目的场地设施如图所示，AB为水平直轨道，上面安装有电动悬挂器，可以载人运动，水面上漂浮着一个半径为R，角速度为ω，铺有海绵垫的转盘，转盘的轴心离平台的水平距离为L，平台边缘与转盘平面的高度差为H．选手抓住悬挂器可以在电动机的带动下，从A点下方的平台边缘处沿水平方向做初速度为零，加速度为a的匀加速直线运动．选手必须作好判断，在合适的位置释放，才能顺利落在转盘上．设人的质量为m（不计身高），人与转盘间的最大静摩擦力为μmg，重力加速度为g．
1．
如图，在水平地面上固定一倾角为θ的光滑绝缘斜面，斜面处于电场强度大小为E、方向沿斜面向下的匀强电场中．一劲度系数为k的绝缘轻质弹簧的一端固定在斜面底端，整根弹簧处于自然状态．一质量为m、带电量为q（q＞0）的滑块从距离弹簧上端为s0处静止释放，滑块在运动过程中电量保持不变，设滑块与弹簧接触后粘在一起不分离且无没有机械能损失，物体刚好返回到S0段中点，弹簧始终处在弹性限度内，重力加速度大小为g．则（ ）
如图，在水平地面上固定一倾角为θ的光滑绝缘斜面，斜面处于电场强度大小为E、方向沿斜面向下的匀强电场中．一劲度系数为k的绝缘轻质弹簧的一端固定在斜面底端，整根弹簧处于自然状态．一质量为m、带电量为q（q＞0）的滑块从距离弹簧上端为s0处静止释放，滑块在运动过程中电量保持不变，设滑块与弹簧接触后粘在一起不分离且无没有机械能损失，物体刚好返回到S0段中点，弹簧始终处在弹性限度内，重力加速度大小为g．则（ ）| A． | 滑块从静止释放到与弹簧上端接触瞬间所经历的时间为t=$\sqrt{\frac{2m{S}_{0}}{qE+mgsinθ}}$ | |
| B． | 滑块运动过程中的最大动能等于（mgsinθ+qE）（$\frac{mgsinθ}{k}$+s0） | |
| C． | 弹簧的最大弹性势能为（mgsinθ+qE）（$\frac{2mgsinθ+2qE}{k}$+$\frac{3{S}_{0}}{2}$） | |
| D． | 运动过程中地球、物体和弹簧组成系统机械能和电势能总和始终不变 |
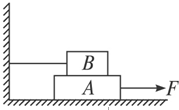如图所示，物体A重40N，物体B重20N，A与B，B与地面间的动摩擦因数均为0.2，当用水平力向右匀速拉动物体A时，要求：
如图是一个多量程多用电表的简化电路图，电流、电压和电阻的测量都各有两个量程不同的档位．电压的大量程是6V，小量程为3V．