题目内容
【题目】如图所示,为一环形磁约束装置的原理图,圆心为原点O、半径为R0的圆形区域Ⅰ内有方向垂直xOy平面向里的匀强磁场。一束质量为m、电荷量为q、初速度为v0的带正电粒子从坐标为(0、R0)的A点沿y负方向射入磁场区域Ⅰ,粒子全部经过x轴上的P点,方向沿x轴正方向。当在环形区域Ⅱ加上方向垂直于xOy平面的匀强磁场时,上述粒子仍从A点沿y轴负方向射入区域Ⅰ,粒子经过区域Ⅱ后从Q点第2次射入区域Ⅰ,已知OQ与x轴正方向成60°。不计重力和粒子间的相互作用。求:
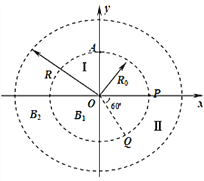
(1)区域Ⅰ中磁感应强度B1的大小;
(2)若要使所有的粒子均约束在区域内,则环形区域Ⅱ中B2的大小、方向及环形半径R至少为多大;
(3)粒子从A点沿y轴负方向射入后至再次以相同的速度经过A点的运动周期。
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) 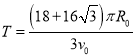
【解析】试题分析:(1)粒子进入磁场Ⅰ做圆周运动,由几何关系求出轨迹半径,由牛顿第二定律求解磁感应强度B1的大小;
(2)在环形区域Ⅱ中,当粒子的运动轨迹与外圆相切,画出轨迹,由几何关系求解轨迹半径,再求解B2的大小.
(3)根据粒子运动的轨迹所对应的圆心角,再求解运动周期.
解:(1)设在区域Ⅰ内轨迹圆半径为r1=R0;
r1=![]()
![]()
所以![]()
(2)设粒子在区域Ⅱ中的轨迹圆半径为r2,部分轨迹如图,由几何关系知:![]() ,
,
![]() ,
,

所以![]() ,
,
方向与B1相反,即垂直xoy平面向外;
由几何关系得:R=2r2+r2=3r2,
即![]()
(3)轨迹从A点到Q点对应圆心角θ=90°+60°=150°,要仍从A点沿y轴负方向射入,需满足;
150n=360m,m、n属于自然数,即取最小整数m=5,n=12
![]() ,其中
,其中![]()
代入数据得:![]()
答:
(1)区域Ⅰ中磁感应强度B1的大小为![]() ;
;
(2)环形区域Ⅱ中B2的大小为![]() 、方向与B1相反,即垂直xoy平面向外;环形半径R至少为
、方向与B1相反,即垂直xoy平面向外;环形半径R至少为![]() R0;
R0;
(3)粒子从A点沿y轴负方向射入后至再次以相同的速度经过A点的运动周期为![]() .
.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案【题目】某同学用如图甲所示装置做探究弹力和弹簧伸长关系的实验.他先测出不挂砝码时弹簧下端指针所指的标尺刻度,然后在弹簧下端挂上砝码,并逐个增加砝码,测出指针所指的标尺刻度,所得数据如表:(重力加速度g取9.8m/s2)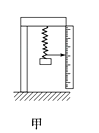
砝码质量m/102g | 0 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 | 7.00 |
标尺刻度x/10﹣2m | 15.00 | 18.94 | 22.82 | 26.78 | 30.66 | 34.60 | 42.00 | 54.50 |
(1)根据所测数据,在图乙中作出弹簧指针所指的标尺刻度x与砝码质量m的关系曲线.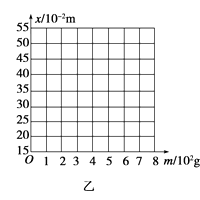
(2)根据所测得的数据和关系曲线可判断,在 N范围内弹力大小与弹簧伸长关系满足胡克定律.这种规格的弹簧劲度系数为N/m.