题目内容
如图6所示,一个质量为M的人站在台秤上,用跨过定滑轮的绳子,将质量为m的物体自高处放下,当物体以a加速下降(a<g=时,台秤的读数为 ( )


| A.(M-m)g+ma | B.(M+m)g-ma |
| C.(M-m)g | D.(M-m)g-m |
A
对人和物体分别进行受力分析后,根据牛顿第二定律写出方程:
对人有:FT+FN=Mg,
对m有:mg-FT=ma
由此解得FN=(M-m)g+ma
利用超重、失重的概念解答是很简捷的,如果物体不动那么绳对物体的拉力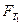 =mg,此时台秤读数
=mg,此时台秤读数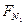 =Mg-
=Mg-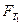 =(M-m)g。当物体以a加速下降时,由于失重,此时绳对物体的拉力FT=m(g-a),所以,此时台秤读数为FN=Mg-FT=(M-m)g+ma。
=(M-m)g。当物体以a加速下降时,由于失重,此时绳对物体的拉力FT=m(g-a),所以,此时台秤读数为FN=Mg-FT=(M-m)g+ma。
对人有:FT+FN=Mg,
对m有:mg-FT=ma
由此解得FN=(M-m)g+ma
利用超重、失重的概念解答是很简捷的,如果物体不动那么绳对物体的拉力
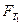 =mg,此时台秤读数
=mg,此时台秤读数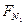 =Mg-
=Mg-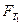 =(M-m)g。当物体以a加速下降时,由于失重,此时绳对物体的拉力FT=m(g-a),所以,此时台秤读数为FN=Mg-FT=(M-m)g+ma。
=(M-m)g。当物体以a加速下降时,由于失重,此时绳对物体的拉力FT=m(g-a),所以,此时台秤读数为FN=Mg-FT=(M-m)g+ma。
练习册系列答案
相关题目