题目内容
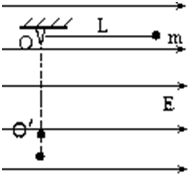 如图所示,长为L的绝缘细线,一端悬于O点,另一端连接一质量为m的带负电小球,置于水平向右的匀强电场中,在O点正下方钉一个钉子O′,已知小球受到的电场力为重力的
如图所示,长为L的绝缘细线,一端悬于O点,另一端连接一质量为m的带负电小球,置于水平向右的匀强电场中,在O点正下方钉一个钉子O′,已知小球受到的电场力为重力的| 1 | ||
|
分析:本题是一个摆在重力场和电场的叠加场中的运动问题,由于重力场和电场力做功都与路径无关,因此可以把两个场叠加起来看成一个等效力场来处理,如图所示,分析小球的运动过程:摆球先沿电场力与重力的合力方向做匀加速直线运动,绳子绷紧瞬间,沿绳子方向的分速度突然减小为零,再以切向分速度绕O′点做圆周运动.在等效力场中,过点O′做合力F的平行线与圆的交点为Q,即为摆球绕O′点做圆周运动的“最高点”,由合力提供向心力,求出“最高点”的临界速度表达式,再结合能量守恒列式求解.
解答: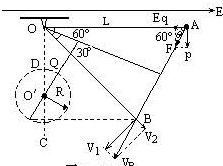 解:由于重力场和电场力做功都与路径无关,因此可以把两个场叠加起来看成一个等效力场来处理,如图所示,有:
解:由于重力场和电场力做功都与路径无关,因此可以把两个场叠加起来看成一个等效力场来处理,如图所示,有:
tanθ=
=
=
得:θ=60°
开始时,摆球在合力F的作用下沿力的方向作匀加速直线运动,从A点运动到B点,由图可知,△AOB为等边三角形,则摆球从A到B,在等效力场中,由能量守恒定律得:F=
m
在B点处,由于在极短的时间内细线被拉紧,摆球受到细线拉力的冲量作用,法向分量v2变为零,切向分量为:
v1=vBcos30°=
vB
接着摆球以v1为初速度沿圆弧BC做变速圆周运动,碰到钉子O′后,在竖直平面内做圆周运动,在等效力场中,过点O′做合力F的平行线与圆的交点为Q,即为摆球绕O′点做圆周运动的“最高点”,在Q点应满足:F=m
根据能量守恒定律得:
m
+(-
FL)=
m
+[-F(L-R)cos30°-R]
联立方程可解得:R=
L
所以得:OO′=L-R=
L
答:OO′长度是
L.
 解:由于重力场和电场力做功都与路径无关,因此可以把两个场叠加起来看成一个等效力场来处理,如图所示,有:
解:由于重力场和电场力做功都与路径无关,因此可以把两个场叠加起来看成一个等效力场来处理,如图所示,有:tanθ=
| mg |
| Eq |
| mg | ||||
|
| 3 |
得:θ=60°
开始时,摆球在合力F的作用下沿力的方向作匀加速直线运动,从A点运动到B点,由图可知,△AOB为等边三角形,则摆球从A到B,在等效力场中,由能量守恒定律得:F=
| 1 |
| 2 |
| v | 2 B |
在B点处,由于在极短的时间内细线被拉紧,摆球受到细线拉力的冲量作用,法向分量v2变为零,切向分量为:
v1=vBcos30°=
| ||
| 2 |
接着摆球以v1为初速度沿圆弧BC做变速圆周运动,碰到钉子O′后,在竖直平面内做圆周运动,在等效力场中,过点O′做合力F的平行线与圆的交点为Q,即为摆球绕O′点做圆周运动的“最高点”,在Q点应满足:F=m
| ||
| R |
根据能量守恒定律得:
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 Q |
联立方程可解得:R=
2
| ||
2
|
所以得:OO′=L-R=
| 5 | ||
2
|
答:OO′长度是
| 5 | ||
2
|
点评:考生以前做过不少“在重力场中释放摆球.摆球沿圆弧线运动的习题”.受到这道题思维定势的影响,没能分析出本题的摆球是在重力场和电场叠加场中运动.小球同时受到重力和电场力的作用,这两个力对摆球运动轨迹都有影响.受“最高点”就是几何上的最高点的思维定势的影响,没能分析清楚物理意义上的“最高点”含义.在重力场中应是重力方向上物体运动轨迹的最高点,恰好是几何意义上的最高点.而本题中,“最高点”则是重力与电场力的合力方向上摆球运动的轨迹的最高点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,在场强为E的水平匀强电场中,一根长为l的绝缘杆,两端分别固定着带有电量+q和-q的小球(大小不计).现让缘绝杆绕中点O逆时针转动α角,则转动中带电小球克服电场力做功为
如图所示,在场强为E的水平匀强电场中,一根长为l的绝缘杆,两端分别固定着带有电量+q和-q的小球(大小不计).现让缘绝杆绕中点O逆时针转动α角,则转动中带电小球克服电场力做功为 如图所示,圆柱形绝热气缸(设其足够长)固定于水平面上,缸内用绝热活塞密封一定质量的理想气体,已知活塞与气缸壁的接触是光滑的,活塞的横截面积为S,大气压强为P0,电源和电热丝构成回路.可以对气体缓慢加热.开始时,电路未接通,系统处于平衡状态,封闭气体的温度为T1.现用两种方法使气缸内气体温度,均由T1缓慢升高到T2.第一次先将活塞固定,接通电路后电热丝产生的热量为Q1;第二次活塞不固定.可以缓慢自由移动,接通电路后电热丝产生的热量为Q2.
如图所示,圆柱形绝热气缸(设其足够长)固定于水平面上,缸内用绝热活塞密封一定质量的理想气体,已知活塞与气缸壁的接触是光滑的,活塞的横截面积为S,大气压强为P0,电源和电热丝构成回路.可以对气体缓慢加热.开始时,电路未接通,系统处于平衡状态,封闭气体的温度为T1.现用两种方法使气缸内气体温度,均由T1缓慢升高到T2.第一次先将活塞固定,接通电路后电热丝产生的热量为Q1;第二次活塞不固定.可以缓慢自由移动,接通电路后电热丝产生的热量为Q2.
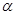 角,则转动中带电小球克服电场力做功为___________.
角,则转动中带电小球克服电场力做功为___________.