题目内容
在“利用打点计时器测定匀加速直线运动加速度”的实验中,打点计时器接在50Hz的低压交变电源上.某同学在打出的纸带上每5个点取一个计数点,共取了A、B、C、D、召、F六个计数点(每相邻两个计数点间的四个点未画出).从每一个计数点处将纸带剪开分成五段,分别为a、b、c、d、e到长紧靠但不重叠地粘在xoy坐标系中,如图1所示,由此可以得到一条表示v-t关系的图线,从而求出加速度的大小.
(1)该同学将纸条上端中心连接起来得到v-t图线,如图2所示.请指出在该图象中哪个轴相当于v轴?答:
(2)若测得a段纸带的长度为2.0cm,e段纸带的长度为10.0cm,可求出加速度的大小为
(3)实际交流电的频率不太稳定,若实验时交流电的频率比50Hz大.则第(2)问求得的加速度与真实值相比
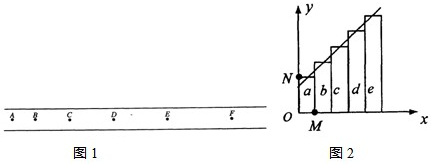
(1)该同学将纸条上端中心连接起来得到v-t图线,如图2所示.请指出在该图象中哪个轴相当于v轴?答:
y轴相当于v轴
y轴相当于v轴
;图线中M点的横坐标和N点的纵坐标分别为0.1s
0.1s
、0.2m/s
0.2m/s
.(2)若测得a段纸带的长度为2.0cm,e段纸带的长度为10.0cm,可求出加速度的大小为
2
2
m/s2.(3)实际交流电的频率不太稳定,若实验时交流电的频率比50Hz大.则第(2)问求得的加速度与真实值相比
偏小
偏小
.(“偏大”“偏小”“不变”)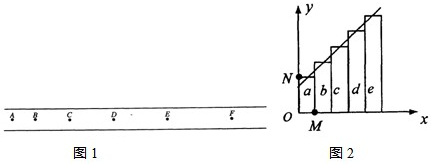
分析:使用的方法是等效代替法解题,它们的长度分别等于x=v平均t,因为剪断的纸带所用的时间都是t=0.1s,即时间t相等,所以纸带的长度之比等于此段纸带的平均速度之比;
而此段纸带的平均速度等于这段纸带中间时刻的速度,最后得出结论纸带的长度之比等于此段纸带的平均速度之比,还等于各段纸带中间时刻的速度之比,即纸带的高度之比等于中间时刻速度之比.
而此段纸带的平均速度等于这段纸带中间时刻的速度,最后得出结论纸带的长度之比等于此段纸带的平均速度之比,还等于各段纸带中间时刻的速度之比,即纸带的高度之比等于中间时刻速度之比.
解答:解:(1)由于纸带的高度之比等于中间时刻速度之比,也就是说图中a段纸带高度代表0.05s时的瞬时速度,b纸带高度代表0.15s时的瞬时速度,c纸带高度代表0.25s时的瞬时速度,d的高度代表0.35s时的瞬时速度,e代表0.45s时的瞬时速度;所以在xoy坐标系中y轴相当于v轴,;
由于剪断的纸带所用的时间都是t=0.1s,所以图线中M点的横坐标表示0.1s,由于a段纸带高度代表0.05s时的瞬时速度,所以N点的纵坐标表示0.05s时刻的瞬时速度.
N点的瞬时速度等于纸带a的平均速度:vN=
m/s=0.2m/s
(2)a段纸带的长度为2.0cm,解得0.05s末的速度vN=0.2m/s;
e段纸带的长度为10.0cm,解得0.45s末的速度:v2=
m/s=1m/s
所以加速度:a=
=
=2m/s2,
(3)若实验时交流电的频率比50Hz大,则打点计时器打出的点时间间隔小于0.02s,计数点间的时间间隔小于0.1s,但是在解题过程中代入的时间间隔为0.1s,即代入了较长的时间.则第(2)问求得的加速偏小.
故答案为:(1)y轴相当于v轴、0.1s、0.2m/s
(2)2
(3)偏小
由于剪断的纸带所用的时间都是t=0.1s,所以图线中M点的横坐标表示0.1s,由于a段纸带高度代表0.05s时的瞬时速度,所以N点的纵坐标表示0.05s时刻的瞬时速度.
N点的瞬时速度等于纸带a的平均速度:vN=
| 2.0×10-2 |
| 0.1 |
(2)a段纸带的长度为2.0cm,解得0.05s末的速度vN=0.2m/s;
e段纸带的长度为10.0cm,解得0.45s末的速度:v2=
| 10.0×10-2 |
| 0.1 |
所以加速度:a=
| △v |
| △t |
| v2-vN |
| 0.45-0.05 |
(3)若实验时交流电的频率比50Hz大,则打点计时器打出的点时间间隔小于0.02s,计数点间的时间间隔小于0.1s,但是在解题过程中代入的时间间隔为0.1s,即代入了较长的时间.则第(2)问求得的加速偏小.
故答案为:(1)y轴相当于v轴、0.1s、0.2m/s
(2)2
(3)偏小
点评:纸带的长度之比等于此段纸带的平均速度之比,还等于各段纸带中间时刻的速度之比,即纸带的高度之比等于中间时刻速度之比.这种等效替代的方法减小了解题难度.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
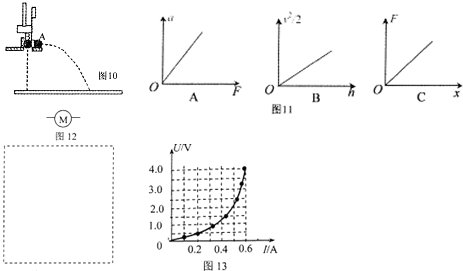

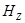 .
.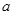 =
=
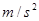 ,纸带上D点相对应的瞬时速度
,纸带上D点相对应的瞬时速度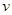 =
= 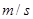 .(结果保留三位有效数字)
.(结果保留三位有效数字)