题目内容
回旋加速器是用来加速带电粒子的装置,图20为回旋加速器的示意图。D1、D2是两个中空的铝制半圆形金属扁盒,在两个D形盒正中间开有一条狭缝,两个D形盒接在高频交流电源上。在D1盒中心A处有粒子源,产生的带正电粒子在两盒之间被电场加速后进入D2盒中。两个D形盒处于与盒面垂直的匀强磁场中,带电粒子在磁场力的作用下做匀速圆周运动,经过半个圆周后,再次到达两盒间的狭缝,控制交流电源电压的周期,保证带电粒子经过狭缝时再次被加速。如此,粒子在做圆周运动的过程中一次一次地经过狭缝,一次一次地被加速,速度越来越大,运动半径也越来越大,最后到达D形盒的边缘,沿切线方向以最大速度被导出。已知带电粒子的电荷量为q,质量为m,加速时狭缝间电压大小恒为U,磁场的磁感应强度为B,D形盒的半径为R,狭缝之间的距离为d。设从粒子源产生的带电粒子的初速度为零,不计粒子受到的重力,求:
(1)带电粒子能被加速的最大动能Ek;
(2)带电粒子在D2盒中第n个半圆的半径;
(3)若带电粒子束从回旋加速器输出时形成的等效电流为I,求从回旋加速器输出的带电粒子的平均功率![]() 。
。

解:
(1)带电粒子在D形盒内做圆周运动,轨道半径达到最大时被引出,此时带电粒子具有最大动能Ek,设离子从D盒边缘离开时的速度为vm。
依据牛顿第二定律 ![]()
所以带电粒子能被加速的最大动能![]() (2分)
(2分)
(2)带电粒子在D2盒中第n个半圆是带电粒子经过窄缝被加速2n-1次后的运动轨道,
设其被加速2n-1次后的速度为vn
由动能定理得 ![]() (2分)
(2分)
此后带电粒子在磁场中做匀速圆周运动,半径为rn
由牛顿第二定律得 ![]() (1分)
(1分)
rn=![]() (1分)
(1分)
(3)设在时间t内离开加速器的带电粒子数N,则正离子束从回旋加速器输出时形成的的等效电流![]() ,解得N=
,解得N=![]()
带电粒子从回旋加速器输出时的平均功率 ![]() =
=![]() (4分)
(4分)

 作业辅导系列答案
作业辅导系列答案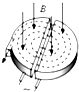 回旋加速器是用来加速带电粒子的装置,如图所示,它的核心部分是两个D形金属盒,两盒相距很近,分别和高频交流电源相连接,两盒间的窄缝中形成匀强电场,使带电粒子每次通过窄缝都得到加速.两盒放在匀强磁场中,磁场方向垂直于盒底面,带电粒子在磁场中做圆周运动,通过两盒间的窄缝时反复被加速,达到最大圆周半径时通过特殊装置被引出.以下关于回旋加速器的原理和应用,下列说法中正确的是( )
回旋加速器是用来加速带电粒子的装置,如图所示,它的核心部分是两个D形金属盒,两盒相距很近,分别和高频交流电源相连接,两盒间的窄缝中形成匀强电场,使带电粒子每次通过窄缝都得到加速.两盒放在匀强磁场中,磁场方向垂直于盒底面,带电粒子在磁场中做圆周运动,通过两盒间的窄缝时反复被加速,达到最大圆周半径时通过特殊装置被引出.以下关于回旋加速器的原理和应用,下列说法中正确的是( )| A、加速同一种带电粒子时,加速电压越大,粒子获得的最大动能越大 | ||||
| B、加速同一种带电粒子时,加速电压的频率越大,粒子获得的最大动能越大 | ||||
| C、加速同一种带电粒子时,D形盒中的磁场越强,粒子获得的最大动能越大 | ||||
D、加速器可以同时加速氚核(
|
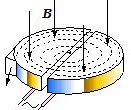 回旋加速器是用来加速带电粒子的装置,如图所示,它的核心部分是两个D形金属盒,两盒相距很近,连接好高频交流电源后,两盒间的窄缝中形成交变的匀强电场,使带电粒子每次通过窄缝都能得到加速.两盒放在匀强磁场中,磁场方向垂直盒面向下,带电粒子在磁场中做圆周运动,通过两盒间的窄缝时反复被加速,当粒子做圆周运动的半径达到最大值时通过特殊装置被引出.如果用磁感应强度不变的同一回旋加速器分别加速同种电性但比荷(
回旋加速器是用来加速带电粒子的装置,如图所示,它的核心部分是两个D形金属盒,两盒相距很近,连接好高频交流电源后,两盒间的窄缝中形成交变的匀强电场,使带电粒子每次通过窄缝都能得到加速.两盒放在匀强磁场中,磁场方向垂直盒面向下,带电粒子在磁场中做圆周运动,通过两盒间的窄缝时反复被加速,当粒子做圆周运动的半径达到最大值时通过特殊装置被引出.如果用磁感应强度不变的同一回旋加速器分别加速同种电性但比荷(| q |
| m |
| A、加速比荷较大的带电粒子所需的交流电源的周期一定较小 |
| B、加速比荷较大的带电粒子所需的交流电源的周期一定较大 |
| C、加速结束后比荷较大的带电粒子获得的最大动能一定较大 |
| D、加速结束后比荷较大的带电粒子获得的最大动能一定较小 |
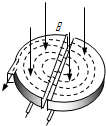 回旋加速器是用来加速带电粒子的装置,如图所示.它的核心部分是两个D形金属盒,两盒相距很近,分别和高频交流电源相连接,两盒间的窄缝中形成匀强电场,使带电粒子每次通过窄缝都得到加速.两盒放在匀强磁场中,磁场方向垂直于盒底面,带电粒子在磁场中做圆周运动,通过两盒间的窄缝时反复被加速,直到达到最大圆周半径时通过特殊装置被引出.如果用同一回旋加速器分别加速氚核(
回旋加速器是用来加速带电粒子的装置,如图所示.它的核心部分是两个D形金属盒,两盒相距很近,分别和高频交流电源相连接,两盒间的窄缝中形成匀强电场,使带电粒子每次通过窄缝都得到加速.两盒放在匀强磁场中,磁场方向垂直于盒底面,带电粒子在磁场中做圆周运动,通过两盒间的窄缝时反复被加速,直到达到最大圆周半径时通过特殊装置被引出.如果用同一回旋加速器分别加速氚核(3 1 |
4 2 |
| A、加速氚核的交流电源的周期较大 |
| B、加速α粒子的交流电源的周期较大 |
| C、加速氚核获得的最大动能也较小 |
| D、加速α粒子获得的最大动能较大 |
 如图所示,回旋加速器是用来加速带电粒子使它获得很大动能的装置.其核心部分是两个“D”型金属盒,置于匀强磁场中,两盒分别与高频交流电源相连.则带电粒子获得的最大动能与下列哪些因素有关( )
如图所示,回旋加速器是用来加速带电粒子使它获得很大动能的装置.其核心部分是两个“D”型金属盒,置于匀强磁场中,两盒分别与高频交流电源相连.则带电粒子获得的最大动能与下列哪些因素有关( ) 回旋加速器是用来加速带电粒子的装置,如图所示.如果用同一回旋加速器分别加速氚核(
回旋加速器是用来加速带电粒子的装置,如图所示.如果用同一回旋加速器分别加速氚核(