题目内容
质量m=50kg的运动员，在一座高桥上做“蹦极”运动．他所用的弹性绳的劲度系数k=62.5N/m，自然长度为l=12m，弹性绳中的弹力与弹性绳的伸长量遵循胡克定律，设在整个运动过程中弹性绳都在弹性限度内．运动员从桥面上由静止自由下落，下落到最低点时（仍在空中），绳的弹性势能Ep=2×104J．不计空气阻力，取g=10m/s2．求：
（1）运动员下落的距离h为多少时达到最大速度．
（2）运动员到达最低点时的加速度a．
（1）运动员下落的距离h为多少时达到最大速度．
（2）运动员到达最低点时的加速度a．
分析：（1）达到最大速度时，弹力和重力平衡，根据平衡条件即可求解；
（2）由机械能守恒定律及牛顿第二定律联立方程即可求解加速度．
（2）由机械能守恒定律及牛顿第二定律联立方程即可求解加速度．
解答：解：（1）达到最大速度时，弹力和重力平衡，故k（h-L）=mg
解出h=20m
（2）设下落的最大高度为h′，由机械能守恒定律：
mg h′=Ep
解出h′=40m
在最低点，由牛顿第二定律得：
K（h′-L）-mg=ma
解得a=25m/s2
答：（1）运动员下落的距离h为20m时达到最大速度．
（2）运动员到达最低点时的加速度为25m/s2．
解出h=20m
（2）设下落的最大高度为h′，由机械能守恒定律：
mg h′=Ep
解出h′=40m
在最低点，由牛顿第二定律得：
K（h′-L）-mg=ma
解得a=25m/s2
答：（1）运动员下落的距离h为20m时达到最大速度．
（2）运动员到达最低点时的加速度为25m/s2．
点评：本题的关键是分析运动员的运动情况，再选择平衡条件、牛顿第二定律等等物理规律求解．
练习册系列答案
相关题目
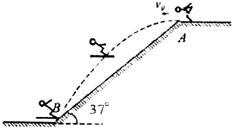跳台滑雪是一种极为壮观的运动，运动员穿着滑雪板，从跳台水平飞出，在空中飞行一段距离后着陆，如图所示．设运动员连同滑雪板的总质量m=50kg，从倾角θ=37°的坡顶A点以速度v0=20m/s沿水平方向飞出，恰落到山坡底的水平商上的B处．（g=10m/s2，sin37°=0.6，cos37°=0.8）求：