题目内容
14. 如图所示,光滑斜面的长为L=1m,高为H=0.6m,质量分别为mA和mB的A、B两小物体用跨过斜面顶端光滑小滑轮的细绳相连,开始时A物体离地高为h=0.5m,B物体恰在斜面底端,静止开始释放它们,B物体滑到斜面顶端时速度恰好减为零,则A、B两物体的质量比mA:mB是( )
如图所示,光滑斜面的长为L=1m,高为H=0.6m,质量分别为mA和mB的A、B两小物体用跨过斜面顶端光滑小滑轮的细绳相连,开始时A物体离地高为h=0.5m,B物体恰在斜面底端,静止开始释放它们,B物体滑到斜面顶端时速度恰好减为零,则A、B两物体的质量比mA:mB是( )| A. | 1:1 | B. | 2:1 | C. | 3:1 | D. | 6:5 |
分析 A下落过程中,系统的机械能守恒.A落地后B的机械能守恒,分段根据机械能守恒定律列式求解.
解答 解:设斜面的倾角为α,则sinα=$\frac{H}{L}$=0.6,cosα=0.8
在A落地前,由系统的机械能守恒定律得:mAgh-mBghsinα=$\frac{1}{2}$(mA+mB)v2…①
在A落地后,由机械能守恒定律得:mBg(L-h)sinα=$\frac{1}{2}$mBv2…②
由②式可解得:v2=2g(L-h)sinα=6,
代入①式得:5mA-3mB=3(mA+mB),
所以mA:mB=3:1.
故选:C.
点评 本题涉及两个过程,必须分段研究.题中A下落时,A、B单个物体机械能不守恒,但二者组成的系统机械能守恒.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
5.远距离送电,已知升压变压器输出电压为U1,功率为P,降压变压器的输入电压为U2,输电线上电压为△U,输电线的线路损耗的热功率P损,则下列正确的是( )


| A. | P=P损 | B. | P损<P | C. | U1=U2 | D. | U1=U2+△U |
2. 如图所示,质量为m的足球在地面1的位置被踢出后落到地面3的位置,在空中达到最高点2的高度为h.重力加速度为g.下列说法正确的是( )
如图所示,质量为m的足球在地面1的位置被踢出后落到地面3的位置,在空中达到最高点2的高度为h.重力加速度为g.下列说法正确的是( )
 如图所示,质量为m的足球在地面1的位置被踢出后落到地面3的位置,在空中达到最高点2的高度为h.重力加速度为g.下列说法正确的是( )
如图所示,质量为m的足球在地面1的位置被踢出后落到地面3的位置,在空中达到最高点2的高度为h.重力加速度为g.下列说法正确的是( )| A. | 足球从1位置到2位置重力做功为mgh | |
| B. | 足球从1位置到2位置克服重力做功为mgh | |
| C. | 足球从2位置到3位置重力势能减小了mgh | |
| D. | 足球从1位置到3位置重力势能减少了mgh |
6.下列有关分子运动的说法,其中正确的是( )
| A. | 当温度升高时,气体分子的速率分布不再是“中间多、两头少” | |
| B. | 高温状态时气体分子的速率一定比低温状态时大 | |
| C. | 0℃的铁和0℃的冰,它们的分子平均动能可能不相同 | |
| D. | 布朗运动是由液体分子对悬浮粒子撞击作用的不平衡引起的 |
4.分别给门的四角钉上大钉子,用电线(有绝缘外皮的导线)沿着4个钉子绕制一个几十匝的大线圈,线圈的两端连在一个指针在表盘中央的电流表上.下列可能发生的现象是( )
| A. | 只要让门面对准正南方放置,电流表里就有电流流过 | |
| B. | 只要让门面对准正西方放置,电流表里就有电流流过 | |
| C. | 无论开门还是关门,电流表都有电流流过 | |
| D. | 开门速度越快,电流表指针偏转角度越大 |

 如图所示,一根不可伸长的轻绳跨过定滑轮,两端各系一个物体,A物体的质量是B物体质量的2倍.不计一切阻力,A物体自H高度处由静止下落,B物体始终在平台上.取地面为参考平面,求:A物体的动能与其重力势能相等时,A物体离地面的高度.
如图所示,一根不可伸长的轻绳跨过定滑轮,两端各系一个物体,A物体的质量是B物体质量的2倍.不计一切阻力,A物体自H高度处由静止下落,B物体始终在平台上.取地面为参考平面,求:A物体的动能与其重力势能相等时,A物体离地面的高度.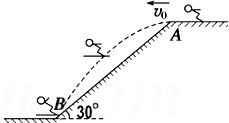 跳台滑雪是一种极为壮观的运动,运动员穿着滑雪板,从跳台水平水平飞出,在空中飞行一段距离后着陆,如图所示,运动员从斜角θ=30°的坡顶A点以某速度沿水平方向飞出,恰落到山坡底的水平面上的B出.已知AB间的距离x=10m.(g=10m/s2,)求:
跳台滑雪是一种极为壮观的运动,运动员穿着滑雪板,从跳台水平水平飞出,在空中飞行一段距离后着陆,如图所示,运动员从斜角θ=30°的坡顶A点以某速度沿水平方向飞出,恰落到山坡底的水平面上的B出.已知AB间的距离x=10m.(g=10m/s2,)求: 如图所示,气缸呈圆柱形,上部有挡板,内部高度为h,筒内一个很薄的质量不计的活塞封闭一定量的理想气体,开始时活塞处于离底部$\frac{2}{3}$h的高度,外界大气压强为pc=1.0×105Pa,温度为27℃,现对气体加热,求:
如图所示,气缸呈圆柱形,上部有挡板,内部高度为h,筒内一个很薄的质量不计的活塞封闭一定量的理想气体,开始时活塞处于离底部$\frac{2}{3}$h的高度,外界大气压强为pc=1.0×105Pa,温度为27℃,现对气体加热,求: