题目内容
如图所示,半径为L1=2m的金属圆环内上、下两部分各有垂直圆环平面的有界匀强磁场,磁感应强度大小均为B1= T.长度也为L1、电阻为R的金属杆ab,一端处于圆环中心,另一端恰好搭接在金属环上,绕着a端做逆时针方向的匀速转动,角速度为ω=
T.长度也为L1、电阻为R的金属杆ab,一端处于圆环中心,另一端恰好搭接在金属环上,绕着a端做逆时针方向的匀速转动,角速度为ω= rad/s.通过导线将金属杆的a端和金属环连接到图示的电路中(连接a端的导线与圆环不接触,图中的定值电阻R1=R,滑片P位于R2的正中央,R2=4R),图中的平行板长度为L2=2m,宽度为d=2m.当金属杆运动到图示位置时,在平行板左边缘中央处刚好有一带电粒子以初速度vo=0.5m/s向右运动,并恰好能从平行板的右边缘飞出,之后进入到有界匀强磁场中,其磁感应强度大小为B2=2T,左边界为图中的虚线位置,右侧及上下范围均足够大.(忽略金属杆与圆环的接触电阻、圆环电阻及导线电阻,忽略电容器的充放电时间,忽略带电粒子在磁场中运动时的电磁辐射等影响,不计平行金属板两端的边缘效应及带电粒子的重力和空气阻力.提示:导体棒以某一端点为圆心匀速转动切割匀强磁场时产生的感应电动势为E=
rad/s.通过导线将金属杆的a端和金属环连接到图示的电路中(连接a端的导线与圆环不接触,图中的定值电阻R1=R,滑片P位于R2的正中央,R2=4R),图中的平行板长度为L2=2m,宽度为d=2m.当金属杆运动到图示位置时,在平行板左边缘中央处刚好有一带电粒子以初速度vo=0.5m/s向右运动,并恰好能从平行板的右边缘飞出,之后进入到有界匀强磁场中,其磁感应强度大小为B2=2T,左边界为图中的虚线位置,右侧及上下范围均足够大.(忽略金属杆与圆环的接触电阻、圆环电阻及导线电阻,忽略电容器的充放电时间,忽略带电粒子在磁场中运动时的电磁辐射等影响,不计平行金属板两端的边缘效应及带电粒子的重力和空气阻力.提示:导体棒以某一端点为圆心匀速转动切割匀强磁场时产生的感应电动势为E= )试分析下列问题:
)试分析下列问题:(1)从图示位置开始金属杆转动半周期的时间内,两极板间的电势差UMN;
(2)带电粒子飞出电场时的速度方向与初速度方向的夹角θ;
(3)带电粒子在电磁场中运动的总时间t总.

【答案】分析:(1)先根据切割公式求出感应电动势,因为电容器是并联在R2的两端,所以电容器两端的电势差大小等于R2两端间的电压,根据闭合电路欧姆定律即可求出R2两端的电压.根据右手定则判断出感应电流的方向,得出M、N两点电势的高低,从而知道UMN的正负.
(2)粒子在平行板电容器内做类平抛运动,在0~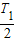 时间内,在水平方向上做匀速直线运动,在竖直方向上做初速度为零的匀加速直线运动,求出出电场时水平方向和竖直方向上的速度,从而求出带电粒子飞出电场时的速度方向与初速度方向的夹角θ.
时间内,在水平方向上做匀速直线运动,在竖直方向上做初速度为零的匀加速直线运动,求出出电场时水平方向和竖直方向上的速度,从而求出带电粒子飞出电场时的速度方向与初速度方向的夹角θ.
(3)求出带电粒子在电场中做类平抛运动,然后进入磁场做匀速圆周运动,最后又返回电场,通过计算知返回电场时,电场方向已反向,在电场中的运动和开始在电场中的运动对称.求出在电场中运动的时间t1,以及求出在磁场中做圆周运动的圆心角,从而求出磁场中运动的时间t2,总时间t总=2t1+t2.
解答: 解:(1)由旋转切割公式得
解:(1)由旋转切割公式得
E=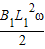 =2 V
=2 V
由电路的连接特点知
E=I?4R
Uo=I?2R=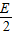 =1 V
=1 V
T1=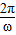 =20 s
=20 s
由右手定则知
在0~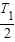 时间内 金属杆ab中的电流方向为b→a,则φa>φb;
时间内 金属杆ab中的电流方向为b→a,则φa>φb;
则 在0~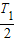 时间内φM<φN UMN=-Uo=-1 V
时间内φM<φN UMN=-Uo=-1 V
(2)粒子在平行板电容器内做类平抛运动,在0~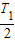 时间内
时间内
水平方向 L2=vo?t1
竖直方向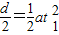
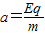
 vy=at1
vy=at1
则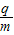 =0.25 C/kg vy=0.5 m/s
=0.25 C/kg vy=0.5 m/s 
tanθ=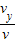 =1 所以 θ=45
=1 所以 θ=45
(3)粒子在匀强磁场中做匀速圆周运动
由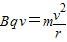 得
得 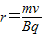 即
即 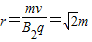
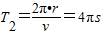
由几何关系及粒子在磁场中运动的对称性可知:粒子恰好在磁场中做了 圆周运动,并且粒子刚好能从平行板电容器的另一极板重新飞回到电场中.则磁场中的运动时间为 t2=
圆周运动,并且粒子刚好能从平行板电容器的另一极板重新飞回到电场中.则磁场中的运动时间为 t2=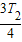 =3π s.由于 t1+t2=4+3π≈13.42 s 大于
=3π s.由于 t1+t2=4+3π≈13.42 s 大于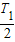 且小于T1 则此时飞回电场时,电场方向与开始时相反,并且此时的速度与飞出电场时的速度等大、与水平方向的夹角大小相同,方向为倾斜左上45,则运动具有对称性,则 t3=t1=4 s.
且小于T1 则此时飞回电场时,电场方向与开始时相反,并且此时的速度与飞出电场时的速度等大、与水平方向的夹角大小相同,方向为倾斜左上45,则运动具有对称性,则 t3=t1=4 s.
综上 带电粒子在电磁场中总的运动时间为 t总=t1+t2+t3=8+3π≈17.42 s.
点评:解决本题的关键掌握右手定则判定感应电流的方向,以及会分析带电粒子在电场中、磁场中所做的运动,在电场中做类平抛运动,在磁场中做匀速圆周运动.
(2)粒子在平行板电容器内做类平抛运动,在0~
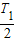 时间内,在水平方向上做匀速直线运动,在竖直方向上做初速度为零的匀加速直线运动,求出出电场时水平方向和竖直方向上的速度,从而求出带电粒子飞出电场时的速度方向与初速度方向的夹角θ.
时间内,在水平方向上做匀速直线运动,在竖直方向上做初速度为零的匀加速直线运动,求出出电场时水平方向和竖直方向上的速度,从而求出带电粒子飞出电场时的速度方向与初速度方向的夹角θ.(3)求出带电粒子在电场中做类平抛运动,然后进入磁场做匀速圆周运动,最后又返回电场,通过计算知返回电场时,电场方向已反向,在电场中的运动和开始在电场中的运动对称.求出在电场中运动的时间t1,以及求出在磁场中做圆周运动的圆心角,从而求出磁场中运动的时间t2,总时间t总=2t1+t2.
解答:
 解:(1)由旋转切割公式得
解:(1)由旋转切割公式得E=
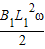 =2 V
=2 V由电路的连接特点知
E=I?4R
Uo=I?2R=
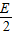 =1 V
=1 VT1=
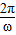 =20 s
=20 s由右手定则知
在0~
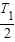 时间内 金属杆ab中的电流方向为b→a,则φa>φb;
时间内 金属杆ab中的电流方向为b→a,则φa>φb;则 在0~
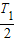 时间内φM<φN UMN=-Uo=-1 V
时间内φM<φN UMN=-Uo=-1 V (2)粒子在平行板电容器内做类平抛运动,在0~
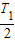 时间内
时间内水平方向 L2=vo?t1
竖直方向
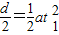
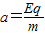
 vy=at1
vy=at1则
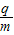 =0.25 C/kg vy=0.5 m/s
=0.25 C/kg vy=0.5 m/s 
tanθ=
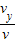 =1 所以 θ=45
=1 所以 θ=45 (3)粒子在匀强磁场中做匀速圆周运动
由
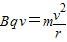 得
得 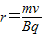 即
即 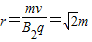
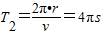
由几何关系及粒子在磁场中运动的对称性可知:粒子恰好在磁场中做了
 圆周运动,并且粒子刚好能从平行板电容器的另一极板重新飞回到电场中.则磁场中的运动时间为 t2=
圆周运动,并且粒子刚好能从平行板电容器的另一极板重新飞回到电场中.则磁场中的运动时间为 t2=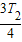 =3π s.由于 t1+t2=4+3π≈13.42 s 大于
=3π s.由于 t1+t2=4+3π≈13.42 s 大于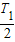 且小于T1 则此时飞回电场时,电场方向与开始时相反,并且此时的速度与飞出电场时的速度等大、与水平方向的夹角大小相同,方向为倾斜左上45,则运动具有对称性,则 t3=t1=4 s.
且小于T1 则此时飞回电场时,电场方向与开始时相反,并且此时的速度与飞出电场时的速度等大、与水平方向的夹角大小相同,方向为倾斜左上45,则运动具有对称性,则 t3=t1=4 s.综上 带电粒子在电磁场中总的运动时间为 t总=t1+t2+t3=8+3π≈17.42 s.
点评:解决本题的关键掌握右手定则判定感应电流的方向,以及会分析带电粒子在电场中、磁场中所做的运动,在电场中做类平抛运动,在磁场中做匀速圆周运动.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



