题目内容
3. 如图所示,一电子(默认初速度为0)经电压U1的加速电场后,垂直且正常通过电压为U2的加速电场,若已知加速电场极板长度为L,极板间距为d,设电子的电荷量为e,质量为m,求电子通过加速电场后的偏转距离和速度偏转角的正切值.
如图所示,一电子(默认初速度为0)经电压U1的加速电场后,垂直且正常通过电压为U2的加速电场,若已知加速电场极板长度为L,极板间距为d,设电子的电荷量为e,质量为m,求电子通过加速电场后的偏转距离和速度偏转角的正切值.
分析 带电粒子在加速电场中做匀加速直线运动,可以用动能定理解出速度,进入偏转电场做类平抛运动,结合平抛运动规律解题:水平方向匀速直线运动,竖直方向初速度为零的匀加速直线运动.
解答 解:(1)粒子由初速为零,经电压为U1电场加速,在加速过程中,只有电场力做的功为qU1,
由动能定理得:qU1=$\frac{1}{2}$mv02
解得:v0=$\sqrt{\frac{2q{U}_{1}}{m}}$
粒子经匀强电场偏转,偏转电场长为L,场强为E=$\frac{{U}_{2}}{d}$,
进入偏转电场做类平抛运动,结合平抛运动规律解题,
水平方向:L=v0t
竖直方向初速度为零的匀加速直线运动:y=$\frac{1}{2}$at2=$\frac{1}{2}$$\frac{qE}{m}$($\frac{L}{{v}_{0}}$)2=$\frac{{U}_{2}{L}^{2}}{4{U}_{1}d}$
(2)由平抛运动规律得:
tanθ=$\frac{{v}_{y}}{{v}_{0}}$=$\frac{at}{{v}_{0}}$=$\frac{{U}_{2}L}{2{U}_{1}}$ 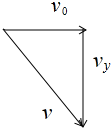
答:电子通过加速电场后的偏转距离$\frac{{U}_{2}{L}^{2}}{4{U}_{1}d}$,和速度偏转角的正切值为$\frac{{U}_{2}L}{2{U}_{1}}$.
点评 注意类平抛运动过程水平方向的运动与竖直方向的运动具有等时性,然后分别应用匀速运动规律和初速度为零匀加速直线运动规律解题.

练习册系列答案
相关题目
13.物体做匀加速直线运动,其加速度是2m/s2,关于这个2m/s2理解正确的是( )
| A. | 某1s末的速度比该1s初的速度大2 m/s | |
| B. | 某1s末的速度比该1s初的速度大2倍 | |
| C. | 某1s初的速度与前1s末的速度相差2 m/s | |
| D. | 某1s末的速度与前1s初的速度总是相差2 m/s |
14. 如图所示,一轻弹簧一端固定于点,另一端系一重物,将重物从与悬点在同一水平面且弹簧保持原长的点无初速度释放,让它自由摆下,不计空气阻力,在重物由A点摆向最低点B的过程中,正确的是( )
如图所示,一轻弹簧一端固定于点,另一端系一重物,将重物从与悬点在同一水平面且弹簧保持原长的点无初速度释放,让它自由摆下,不计空气阻力,在重物由A点摆向最低点B的过程中,正确的是( )
 如图所示,一轻弹簧一端固定于点,另一端系一重物,将重物从与悬点在同一水平面且弹簧保持原长的点无初速度释放,让它自由摆下,不计空气阻力,在重物由A点摆向最低点B的过程中,正确的是( )
如图所示,一轻弹簧一端固定于点,另一端系一重物,将重物从与悬点在同一水平面且弹簧保持原长的点无初速度释放,让它自由摆下,不计空气阻力,在重物由A点摆向最低点B的过程中,正确的是( )| A. | 弹簧弹力总与速度方向垂直,故弹力不做功 | |
| B. | 重物的重力势能减小,弹簧的弹性势能增大 | |
| C. | 若用与弹簧原长相等的细绳代替弹簧后,重力做正功,弹力不做功 | |
| D. | 若用与弹簧原长相等的细绳代替弹簧后,重力做功不变,弹力不做功 |
11. 沿竖直方向上下振动的简谐运动的质点P在0-4s时间内的振动图象,正确的是(向上为正)( )
沿竖直方向上下振动的简谐运动的质点P在0-4s时间内的振动图象,正确的是(向上为正)( )
 沿竖直方向上下振动的简谐运动的质点P在0-4s时间内的振动图象,正确的是(向上为正)( )
沿竖直方向上下振动的简谐运动的质点P在0-4s时间内的振动图象,正确的是(向上为正)( )| A. | 质点在t=1s时刻速度方向向上 | |
| B. | 质点在t=2s时刻速度为零 | |
| C. | 质点在t=3s时刻加速度方向向下 | |
| D. | 质点在t=4s时刻回复力为零,速度最大 |
15.如果a-$\frac{1}{m}$图象是通过原点的一条直线,则说明( )
| A. | 物体的加速度a与物体的质量m成正比 | |
| B. | 物体的加速度a与物体的质量m成反比 | |
| C. | 物体的质量m与物体的加速度a成正比 | |
| D. | 物体的质量m与物体的加速度a成反比 |
12.两个电量不同的正离子,被同一电场加速后垂直进入同一偏转电场,下列说法正确的是( )
| A. | 比荷$\frac{q}{m}$大的正离子离开偏转电场时的偏转角大 | |
| B. | 比荷$\frac{q}{m}$大的正离子离开偏转电场时的偏转角小 | |
| C. | 比荷$\frac{q}{m}$不同的正离子离开偏转电场时速度方向相同 | |
| D. | 带电量大的正离子离开偏转电场时的偏转角大 |
 如图所示,设A、B为地球赤道圆的一条直径的两端,利用同步卫星将一电磁波信号由A点传到B点,已知地球半径为R,地球表面处的重力加速度为g,地球自转周期为T,不考虑大气对电磁波的折射.设电磁波在空气中的传播速度为c.求:
如图所示,设A、B为地球赤道圆的一条直径的两端,利用同步卫星将一电磁波信号由A点传到B点,已知地球半径为R,地球表面处的重力加速度为g,地球自转周期为T,不考虑大气对电磁波的折射.设电磁波在空气中的传播速度为c.求:



 建立如图所示的直角坐标系xoy,在第二象限内有电场强度大小为E、方向与x轴正方向成45°的匀强电场,在第一象限内有电场强度大小也为E、方向与y轴负方向成45°的匀强电场;现有质量为m、电荷量为q的正粒子(重力不计)从A(-L,0)处静止释放.
建立如图所示的直角坐标系xoy,在第二象限内有电场强度大小为E、方向与x轴正方向成45°的匀强电场,在第一象限内有电场强度大小也为E、方向与y轴负方向成45°的匀强电场;现有质量为m、电荷量为q的正粒子(重力不计)从A(-L,0)处静止释放.