题目内容
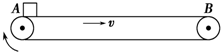
一质量为m=4kg的长木板静止在水平面上,长木板与水平地面间的动摩擦因数为0.1,一质量为2kg的小物块(可视为质点),从长木板左端以6m/s的水平速度开始沿长木板滑动,如图所示.由于摩擦的缘故,小物块恰好停在长木板的右端,已知小物块与长木板间的动摩擦因数为0.4,求:
(1)小物块和长木板的加速度大小和方向;
(2)当长木板的速度刚好与小物块的速度相同时,长木板运动的时间;
(3)长木板的长度.
(1)小物块和长木板的加速度大小和方向;
(2)当长木板的速度刚好与小物块的速度相同时,长木板运动的时间;
(3)长木板的长度.

(1)根据牛顿第二定律,小物块的加速度大小为:a1=
=μ1g=4m/s2,方向与v1方向相反;
长木板的加速度大小为:a2=
=
=0.5m/s2,方向与v1同向;
(2)设经过时间t长木板与小物块刚好达到相同的速度.
经过时间t小物块的速度大小为v=v1-a1t;
经过时间t长木板的速度大小为v=a2t;
解得t=
s≈1.3s;
(3)当小物块与长木板达到相同速度后,二者一起以相同的加速度做匀减速运动,直至停止.
由题意可分析得出,当二者速度刚好相等时,小物块恰好运动到长木板的右端.
经过时间t小物块的位移为x1=v1t-
a1t2;
经过时间t长木板的位移为x2=
a2t2;
长木板的长度为L=x1-x2=4m;
答:(1)小物块的加速度大小为4m/s2,方向与速度反向;长木板的加速度大小为0.5m/s2,方向与速度方向相同;
(2)当长木板的速度刚好与小物块的速度相同时,长木板运动的时间为1.3s;
(3)长木板的长度为4m.
| f1 |
| m1 |
长木板的加速度大小为:a2=
| f1-f |
| m |
| μ1m1g-μ(m1+m)g |
| m |
(2)设经过时间t长木板与小物块刚好达到相同的速度.
经过时间t小物块的速度大小为v=v1-a1t;
经过时间t长木板的速度大小为v=a2t;
解得t=
| 4 |
| 3 |
(3)当小物块与长木板达到相同速度后,二者一起以相同的加速度做匀减速运动,直至停止.
由题意可分析得出,当二者速度刚好相等时,小物块恰好运动到长木板的右端.
经过时间t小物块的位移为x1=v1t-
| 1 |
| 2 |
经过时间t长木板的位移为x2=
| 1 |
| 2 |
长木板的长度为L=x1-x2=4m;
答:(1)小物块的加速度大小为4m/s2,方向与速度反向;长木板的加速度大小为0.5m/s2,方向与速度方向相同;
(2)当长木板的速度刚好与小物块的速度相同时,长木板运动的时间为1.3s;
(3)长木板的长度为4m.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 水平传送带被广泛地应用于机场和火车站,如图所示为一水平传送带装置示意图.紧绷的传送带AB始终保持恒定的速率v=1m/s运行,一质量为m=4kg的行李无初速度地放在A处,传送带对行李的滑动摩擦力使行李开始做匀加速直线运动,随后行李又以与传送带相等的速率做匀速直线运动.设行李与传送带之间的动摩擦因数μ=0.1,A、B间的距离L=2m,g取10m/s2.求:
水平传送带被广泛地应用于机场和火车站,如图所示为一水平传送带装置示意图.紧绷的传送带AB始终保持恒定的速率v=1m/s运行,一质量为m=4kg的行李无初速度地放在A处,传送带对行李的滑动摩擦力使行李开始做匀加速直线运动,随后行李又以与传送带相等的速率做匀速直线运动.设行李与传送带之间的动摩擦因数μ=0.1,A、B间的距离L=2m,g取10m/s2.求: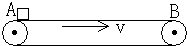 水平传送带被广泛地应用于机场和火车站,用于对旅客的行李进行了安全检查.右图为一水平传送带装置示意图,绷紧的传送带AB始终保持v=1m/s的恒定速率运行,一质量为m=4kg的行李无初速地放在A处,传送带对行李的滑动摩擦力使行李开始做匀加速直线运动,随后行李又以与传送带相等的速率做匀速直线运动.设行李与传送带间的动摩擦因数μ=0.1,AB间的距离L=2m,g取10m/s2.求:
水平传送带被广泛地应用于机场和火车站,用于对旅客的行李进行了安全检查.右图为一水平传送带装置示意图,绷紧的传送带AB始终保持v=1m/s的恒定速率运行,一质量为m=4kg的行李无初速地放在A处,传送带对行李的滑动摩擦力使行李开始做匀加速直线运动,随后行李又以与传送带相等的速率做匀速直线运动.设行李与传送带间的动摩擦因数μ=0.1,AB间的距离L=2m,g取10m/s2.求: 如图所示,在水平地面上有一个长L=1.5m,高h=0.8m的长方体木箱,其质量为M=1kg,与地面的动摩擦因数μ=0.3.在它的上表面的左端放有一质量为m=4kg的小铁块,铁块与木箱的摩擦不计.开始它们均静止.现对木箱施加一水平向左的恒力F=27N.(g=10m/s2)问:
如图所示,在水平地面上有一个长L=1.5m,高h=0.8m的长方体木箱,其质量为M=1kg,与地面的动摩擦因数μ=0.3.在它的上表面的左端放有一质量为m=4kg的小铁块,铁块与木箱的摩擦不计.开始它们均静止.现对木箱施加一水平向左的恒力F=27N.(g=10m/s2)问: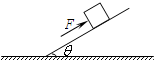 如图,一质量为m=4kg的物体放在一倾角为θ=370的斜面上,当用一沿斜面向上的力F=30.4N推它时,恰能沿斜面向上作匀速直线运动,求
如图,一质量为m=4kg的物体放在一倾角为θ=370的斜面上,当用一沿斜面向上的力F=30.4N推它时,恰能沿斜面向上作匀速直线运动,求