题目内容
如图所示，AB是足够长的倾角为θ倾斜直轨道，BCD是半径为R的光滑圆弧轨道，它们在B点相切。P点与圆弧的圆心O等高，D、E与O点在同一条竖直直径上。一个质量为m的物体（可以看作质点）从AB轨道上的某点由静止释放。
（1）若轨道AB光滑，为使物体能到达圆弧轨道的最高点D，释放点距B点的距离L至少应为多少；
（2）若轨道AB动摩擦因数为μ，物体从P点释放，则它在整个运动过程中在AB轨道上运动的总路程s为多少；
（3）最终当物体通过圆弧轨道最低点E时，对圆弧轨道的压力的大小.
 |
解析：（1）设物体刚好到D点，则mg＝
对全过程由动能定理得：mgLsin θ－mgR（1＋cos θ）＝
mv
得：L=
（2）因为摩擦力始终对物体做负功，所以物体最终在圆心角为2θ的圆弧上往复运动．
对整个过程由动能定理得：mgR·cosθ－μmgcosθ·s＝0 所以总路程为s＝
-
（3）对B→E过程mgR（1－cos θ）＝mv
N－mg＝
由牛顿第三定律，物体对轨道的压力
得对轨道压力：
＝（3－2cosθ）mg
练习册系列答案
相关题目
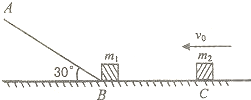如图所示，AB是倾角为30°足够长的光滑斜面，BC是足够长的光滑水平面，且在B点与斜面平滑连接，质量m1=0.2kg的滑块嚣于B点，质量m2=0.1kg的滑块以v0=9m/s速度向左运动并与m1发生撞碰，碰撞过程中没有机械能损失，且ml通过B点前后速率不变，将滑块视为质点，以下判断正确的是（g=10m/s2）（ ）
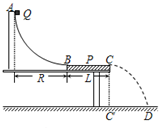测量小物块Q与平板P之间的动摩擦因数的实验装置如图所示．AB是半径足够大的、光滑的四分之一圆弧轨道，与水平固定放置的P板的上表面BC在B点相切，C点在水平地面的垂直投影为C′．重力加速度为g．实验步骤如下：
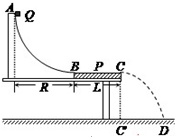测量小物块Q与平板P之间的动摩擦因数的实验装置如图所示．AB是半径足够大的、光滑的四分之一圆弧轨道，与水平固定放置的P板的上表面BC在B点相切，C点在水平地面的垂直投影为C′．重力加速度为g．实验步骤如下：
