题目内容
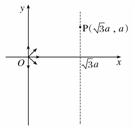
如右图,在0≤x≤a区域内存在与xy平面垂直的匀强磁场,磁感应强度的大小为B.在t=0时刻,一位于坐标原点的粒子源在xy平面内发射出大量同种带电粒子,所有粒子的初速度大小相同,方向与y轴正方向的夹角分布在0~180°范围内.已知沿y轴正方向发射的粒子在t=t0时刻刚好从磁场边界上P(a,a)点离开磁场.
求:
1.粒子在磁场中做圆周运动半径及速度;
2.粒子的比荷q/m;
3.从粒子发射到全部粒子离开磁场所用的时间.
1.
2.
3.2t0
解析:(1)粒子沿y轴的正方向进入磁场,从P点经过做OP的垂直平分线与x轴的交点为圆心,
根据直角三角形有R2=a2+(a-R)2
解得R=a
sinθ==,
则粒子做圆周运动的圆心角为120°,周期为T=3t0
v=,所以v=
(2)粒子做圆周运动的向心力由洛伦兹力提供,根据牛顿第二定律得
Bqv=m()2R,
化简得=.
(3)在磁场中运动时间最长的粒子的轨迹应该与磁场的右边界相切,在三角形中两个相等的腰为R=a,而它的高是h=a-a=a,半径与y轴的夹角是30°,这种粒子的圆心角是240°.所用时间为2t0.
所以从粒子发射到全部离开所用时间为2t0.

练习册系列答案
相关题目
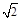 s
s
