Question

【题目】半径为R的光滑绝缘圆环固定在竖直平面内，并且处于水平向右的匀强电场E和垂直于纸面向外的匀强磁场B中．环上套有一个质量为m的带电小球，让小球从与环心等高的P点由静止释放，恰好能滑到圆环的最高点A．求：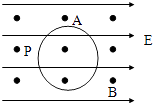

（1）小球的带电性质和带电量．
（2）小球运动过程中对环的最大压力．

Answer 1

【答案】
（1）解：小球在沿圆环运动的过程中，只有重力和电场力做功，在小球从P点到达A点的过程中，重力做负功，电场力必做正功，故小球带正电

因小球恰好到达A点，故小球在A点的速度为零，有：

qER﹣mgR=0

解得：q= ．

答：小球的带带正电和带电量 ．

（2）解：小球到达等效最低点时的压力才最大，设此时速度为v，受到环的压力为N，则：

qE （R+Rcos45°）+mg Rcos45°= mv2

N﹣qvB﹣qEcos45°﹣mgcos45°=m

解得：N=（2+3 ）mg+ mg

由牛顿第三定律得小球对环的压力为（2+3 ）mg+ mg．

答：小球运动过程中对环的最大压力为（2+3 ）mg+ mg．

【解析】（1）根据小球运动情况来确定重力与电场力的关系，从而结合电场强度的方向来确定小球带何种电荷，并由受力平衡条件来算出小球带电量；（2）由于小球始终受到重力与电场力，所以可以等效成一个力，从而与只受重力情况相类比，确定小球运动过程中对环的最大压力的位置及大小．
【考点精析】本题主要考查了动能定理的综合应用和洛伦兹力的相关知识点，需要掌握应用动能定理只考虑初、末状态，没有守恒条件的限制，也不受力的性质和物理过程的变化的影响.所以，凡涉及力和位移，而不涉及力的作用时间的动力学问题，都可以用动能定理分析和解答，而且一般都比用牛顿运动定律和机械能守恒定律简捷；洛伦兹力始终垂直于v的方向，所以洛伦兹力一定不做功才能正确解答此题．