题目内容
4.一违章汽车以速度v1匀速行驶,警车在汽车经过它时开始启动,先以加速度a匀加速运动,匀加速能达到的最大速度为v2,要求警车尽快追上汽车(v2>v1),求:(1)警车追上汽车前与汽车的最远距离?
(2)经过多长时间警车追上汽车?
分析 (1)当两者速度相等时相距最远
(2)根据警车与违章车的位移关系,利用好位移时间公式求的经历的时间
解答 解:(1)当速度相等时两车距离最大,故经历的时间为t则at=v1,解得:t=$\frac{{v}_{1}}{a}$,
在时间t内两车的位移为:
${x}_{1}=\frac{1}{2}a{t}^{2}=\frac{{v}_{1}^{2}}{2a}$,
${x}_{2}={v}_{1}t=\frac{{v}_{1}^{2}}{a}$,
故有:$△x={x}_{2}-{x}_{1}=\frac{{v}_{1}^{2}}{2a}$
(2)警车达到最大速度所需时间为t′,即:$t′=\frac{{v}_{2}}{a}$
在t′内警车通过的位移为${x}_{警}=\frac{{v}_{2}^{2}}{2a}$,违章车通过的位移为${x}_{违}={v}_{1}t=\frac{{v}_{1}{v}_{2}}{a}$,当x警=x违时,所需时间为:t=t$′=\frac{{v}_{2}}{a}$
当x警>x违时,设经历时间为t″,则$\frac{1}{2}at{″}^{2}={v}_{1}t″$,
解得:$t″=\frac{2{v}_{1}}{a}$
当x警<x违时,设经历时间为t总,则${v}_{1}{t}_{总}=\frac{{v}_{2}^{2}}{2a}+{v}_{2}({t}_{总}-\frac{{v}_{2}}{a})$,
解得:${t}_{总}=\frac{{v}_{2}^{2}}{2a({v}_{2}-{v}_{1})}$
答:(1)警车追上汽车前与汽车的最远距离为$\frac{{v}_{1}^{2}}{2a}$
(2)警车追上汽车可能的时间为$\frac{{v}_{2}}{a}$或者$\frac{2{v}_{1}}{a}$,或者$\frac{{v}_{2}^{2}}{2a({v}_{2}-{v}_{1})}$
点评 本题主要考查了追击相遇问题,关键是在第二问中抓住位移相等时警车的速度是否达到最大速度即可

 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案 如图所示,倾角为30°的斜面上固定一半圆球,一圆球也放置在斜面上与半圆球接触并处于静止状态,圆球表面光滑,半圆球和圆球的半径相等,圆球的质量为m.重力加速度为g,则圆球对半圆球的压力为( )
如图所示,倾角为30°的斜面上固定一半圆球,一圆球也放置在斜面上与半圆球接触并处于静止状态,圆球表面光滑,半圆球和圆球的半径相等,圆球的质量为m.重力加速度为g,则圆球对半圆球的压力为( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$mg | C. | $\frac{2\sqrt{3}}{3}$mg | D. | $\frac{\sqrt{3}}{3}$mg |
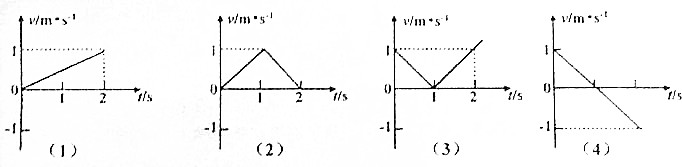
| A. | 在第1秒内,质点(1)(2)的加速度相同 | |
| B. | 在第2秒末,质点(1)(4)回到出发点 | |
| C. | 在前2秒内,质点(2)(3)的平均速度相同 | |
| D. | 在第2秒末,质点(1)(3)离出发点位移相同 |
| A. | kg•A2•m3 | B. | kg•A-2•m3 | C. | N•m2•C-2 | D. | N•m2•A-2 |
 如图所示,编号为Ⅰ、Ⅱ、Ⅲ的三根圆木粗细相同,质量均为m,Ⅱ、Ⅲ并排横放在水平地面上,Ⅰ叠放在Ⅱ、Ⅲ上面,三根圆木均处于静止状态.已知重力加速度g,以下判断正确的是( )
如图所示,编号为Ⅰ、Ⅱ、Ⅲ的三根圆木粗细相同,质量均为m,Ⅱ、Ⅲ并排横放在水平地面上,Ⅰ叠放在Ⅱ、Ⅲ上面,三根圆木均处于静止状态.已知重力加速度g,以下判断正确的是( )| A. | 地面对Ⅱ的摩擦力大小为$\frac{\sqrt{3}}{6}$mg | B. | 地面对Ⅲ的摩擦力大小为0 | ||
| C. | Ⅱ对Ⅰ的支持力大小为$\frac{1}{2}$mg | D. | Ⅲ对Ⅰ的支持力大小为$\frac{\sqrt{3}}{6}$mg |
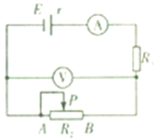 图中的电流表、电压表都是理想的,滑片P从A向B滑动的过程中,下列关于电表示数变化的描述正确的是( )
图中的电流表、电压表都是理想的,滑片P从A向B滑动的过程中,下列关于电表示数变化的描述正确的是( )| A. | 电压表V的示数变大,电流表A的示数变小 | |
| B. | 电压表V的示数变小,电流表A的示数变大 | |
| C. | 电压表V和电流表A的示数都变大 | |
| D. | 电压表V和电流表A的示数都变小 |
| A. | 元电荷就是电子 | |
| B. | 元电荷就是质子 | |
| C. | 元电荷所带电量是物体所带电量的最小单元 | |
| D. | 物体所带电量可以不是元电荷的整数倍 |
| A. | 物体的速度方向为正时,加速度方向也为正 | |
| B. | 物体的速度变化量为正时,加速度方向也为正 | |
| C. | 物体的速度变化量越大,加速度越大 | |
| D. | 物体的速度变化越快,加速度越大 |