题目内容
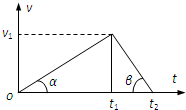 (2006?虹口区二模)一辆汽车做直线运动,t2s末静止,其v-t图如图.图中α<β,若汽车牵引力做功为W,平均功率为P,汽车加速过程和减速过程中克服摩擦力作功分别为W1和W2、平均功率分别为P1、P2,则( )
(2006?虹口区二模)一辆汽车做直线运动,t2s末静止,其v-t图如图.图中α<β,若汽车牵引力做功为W,平均功率为P,汽车加速过程和减速过程中克服摩擦力作功分别为W1和W2、平均功率分别为P1、P2,则( )分析:由动能定理可得出汽车牵引力的功与克服摩擦力做功的关系,由功的公式可求得加速和减速过程中克服摩擦力做功的大小;由摩擦力做功利用P=FV可求得摩擦力的功率关系.
解答:解:A、由动能定理可知W-W1-W2=0,故W=W1+W2;故A正确;
B、由图可知,加速过程的位移要大于减速过程的位移,因摩擦力不变,故加速时摩擦力所做的功大于减速时摩擦力所做的功,即W1>W2,故B正确;
由功能关系可知W=Pt1=P1t1+P2t2 而P1=P2;故P≠P1;故C错误;
因加速和减速运动中,平均速度相等,故由P=FV可知,摩擦力的功率相等,故P1=P2;故D正确;
故选ABD.
B、由图可知,加速过程的位移要大于减速过程的位移,因摩擦力不变,故加速时摩擦力所做的功大于减速时摩擦力所做的功,即W1>W2,故B正确;
由功能关系可知W=Pt1=P1t1+P2t2 而P1=P2;故P≠P1;故C错误;
因加速和减速运动中,平均速度相等,故由P=FV可知,摩擦力的功率相等,故P1=P2;故D正确;
故选ABD.
点评:本题要注意在机车起动中灵活利用功率公式及动能定理公式,同时要注意图象在题目中的应用.

练习册系列答案
相关题目
 (2006?虹口区二模)如图所示,某同学在夏天游玩时,看见湖水中鱼儿戏水时吐出小气泡的情景,觉得很美,于是画了一幅画,但边上的同学认为他画的气泡不符合实际,请根据你所掌握的物理知识指出正确的画法(用简单的文字表述,不要画图),并指出这样画的物理学依据(假设湖水温度不变).
(2006?虹口区二模)如图所示,某同学在夏天游玩时,看见湖水中鱼儿戏水时吐出小气泡的情景,觉得很美,于是画了一幅画,但边上的同学认为他画的气泡不符合实际,请根据你所掌握的物理知识指出正确的画法(用简单的文字表述,不要画图),并指出这样画的物理学依据(假设湖水温度不变).