题目内容
9. 现要测量某一待测电阻Rx的阻,给定的器材有:
现要测量某一待测电阻Rx的阻,给定的器材有:A.待测电阻Rx:阻值约为200Ω
B.电源E:电动势约为1.5V,内阻可忽略不计
C.电流表A1:量程为0~10mA,内电阻r=20Ω
D.电流表A2:量程为0~20mA,内电阻约为8Ω
E.定值电阻R0:阻值R0=80Ω
F.滑动变阻器R:最大阻值为50Ω
G.单刀单掷开关S,导线若干
(1)为了测量电阻Rx,请设计实验电路原理图,画在虚线框内,要求在实验过程中电表的示数从零开始变化,且测量结果尽量准确.
(2)若某次测量中电流表A1的示数为I1,电流表A2的示数为I2,则Rx的表达式为:Rx=$\frac{{{I}_{1}^{\;}(R}_{0}^{\;}+r)}{{I}_{2}^{\;}{-I}_{1}^{\;}}$(用I1、I2、R0、r表示).
分析 由于没有电压表,可考虑将内阻为定值的电流表与定值电阻串联而改装为电压表;然后将改装后的电压表与待测电阻并联再与另一电流表串联,但需要通过估算是否可行;再根据电流要求从零调,可知变阻器应采用分压式接法,即可求解.
解答 解:(1)根据题意,${A}_{1}^{\;}$内阻为确定值,可考虑将${A}_{1}^{\;}$与定值电阻${R}_{0}^{\;}$串联改装为电压表,可得总电压为U=${I}_{A1}^{\;}(r{+R}_{0}^{\;})$=10×10-3×(20+80)V=1V,可以进行实验;
然后判断能否将改装后的电压表与待测电阻并联然后再与${A}_{2}^{\;}$串联:由于此时可求出它们的总电流为${I}_{总}^{\;}$=${I}_{A1}^{\;}+\frac{U}{{R}_{x}^{\;}}$=10mA+$\frac{1}{200}×1000mA$=15mA,与电流表${A}_{2}^{\;}$的量程接近,所以方案可行;又要求电流从零开始,所以变阻器应用分压式接法,电路图如图所示:
(2)根据欧姆定律可得${I}_{2}^{\;}$=${I}_{1}^{\;}$+$\frac{{I}_{1}^{\;}(r{+R}_{0}^{\;})}{{R}_{x}^{\;}}$,解得${R}_{x}^{\;}$=$\frac{{{I}_{1}^{\;}(R}_{0}^{\;}+r)}{{I}_{2}^{\;}{-I}_{1}^{\;}}$.
故答案为:(1)如图,②$\frac{{{I}_{1}^{\;}(R}_{0}^{\;}+r)}{{I}_{2}^{\;}{-I}_{1}^{\;}}$.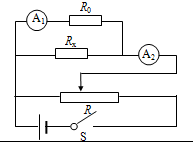
点评 遇到电学实验设计题目,当只给出两个电流表时,应考虑能否将其中一个电流表改装为电压表,改装时,应改装内阻为定值的电流表,画出电路图,然后经过计算检验方案是否可行.

 阅读快车系列答案
阅读快车系列答案| A. | 24m/s 6m/s2 | B. | 24m/s 12m/s2 | C. | 24m/s2 3m/s | D. | 6m/s 24m/s2 |
| A. | 无论接不接入外电路,蓄电池两极间的电压都为2 V | |
| B. | 蓄电池内每通过1 C电荷量,电源把2 J的化学能转变为内能 | |
| C. | 蓄电池在1 s内将2 J的化学能转变为电能 | |
| D. | 蓄电池将化学能转变为电能的本领比一节干电池(电动势为1.5 V)的大 |
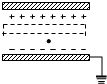 一平行板电容器充电后与电源断开,负极板接地,在两极板间有一正电荷(电量很小)固定在A点,如图所示.以E表示两极板间的场强,U表示电容器的电压,EPA表示正电荷在P点的电势能,若保持负极板不动,将正极板移到图中虚线所示的位置,则( )
一平行板电容器充电后与电源断开,负极板接地,在两极板间有一正电荷(电量很小)固定在A点,如图所示.以E表示两极板间的场强,U表示电容器的电压,EPA表示正电荷在P点的电势能,若保持负极板不动,将正极板移到图中虚线所示的位置,则( )| A. | U变大,E不变 | B. | E不变,EPA不变 | C. | U变小,EPA不变 | D. | U不变,EPA变大 |
| A. | 研究乒乓球运动员打球过程中旋转运动的乒乓球时 | |
| B. | 用GPS定位系统确定汽车位置时 | |
| C. | 研究绕太阳公转的火星时 | |
| D. | 计算一列火车通过铁路大桥所用时间的问题中的火车 |
| A. | 任意1s内的速度增量都是1m/s | B. | 任意相邻的1s 内位移差都是2m | ||
| C. | 前2s内的平均速度是6m/s | D. | 第1s内的位移是5m |
 让一质量为m=1kg的小球从某一高度水平抛出,从小球水平抛出到落地过程中,小球速度方向与水平方向间夹角θ的正切值tanθ随时间t变化的关系图象如图所示.重力加速度g=10m/s2,则( )
让一质量为m=1kg的小球从某一高度水平抛出,从小球水平抛出到落地过程中,小球速度方向与水平方向间夹角θ的正切值tanθ随时间t变化的关系图象如图所示.重力加速度g=10m/s2,则( )| A. | 小球水平抛出的初速度为2m/s | B. | 小球抛出点的高度为20m | ||
| C. | 小球落地时的速度大小为20m/s | D. | 小球落地时的动能为425J |
 电梯上升运动的v-t图象如图所示,从图象可知电梯上升前2s的加速度a=3m/s2,前6s位移S=39m,前6S的平均速度V=6.5m/s.
电梯上升运动的v-t图象如图所示,从图象可知电梯上升前2s的加速度a=3m/s2,前6s位移S=39m,前6S的平均速度V=6.5m/s. 如图所示,物体以100J的初动能从斜面底端向上运动,当它通过斜面某一点M时,其动能减少80J,机械能减少32J,如果物体能从斜面上返回底端,则物体到达底端时的动能为( )
如图所示,物体以100J的初动能从斜面底端向上运动,当它通过斜面某一点M时,其动能减少80J,机械能减少32J,如果物体能从斜面上返回底端,则物体到达底端时的动能为( )