题目内容
一个质量可不计的活塞将一定量的理想气体封闭在上端开口的直立圆筒形气缸内,活塞上堆放着铁砂,如图14-2-9所示,最初活塞搁置在气缸内壁的固定卡环上,气体柱的高度为H0,压强等于大气压强p0.现对气体缓慢加热,当气体温度升高了ΔT=60 K时,活塞(及铁砂)开始离开卡环而上升,继续加热直到气柱高度为H1=1.5H0.此后,在维持温度不变的条件下逐渐取走铁砂,直到铁砂全部取走时,气柱高度变为H2=1.8H0,求此时气体的温度 .(不计活塞与气缸之间的摩擦)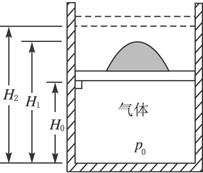
图14-2-9
解析:设气体最初温度为T0,则活塞刚离开卡环时温度为T0+ΔT,压强为p1.由等容升温过程得
![]() =
=![]() ①
①
设气柱高度为H1时温度为T1,由等压升温过程得
![]() =
=![]() ②
②
设气柱高度为H2时温度为T2,由等温膨胀过程(T2=T1)得
![]() =
=![]() ③
③
由①和③两式求得
![]() =
=![]() ④
④
解得 T0=![]() ΔT ⑤
ΔT ⑤
由②和④两式得
![]() =
=![]() ,或T1=
,或T1=![]() T0 ⑥
T0 ⑥
将⑤式代入⑥式,并利用T2=T1,得
T2=T1=![]() ΔT ⑦
ΔT ⑦
代入数字得T2=540 K.
答案:540 K

练习册系列答案
相关题目
 如图所示,一个质量可不计的活塞将一定量的理想气体封闭在上端开口的直立圆筒形气缸内,活塞上堆放着铁砂,最初活塞搁置在气缸内壁的固定卡环上,气体柱的高度为H0=10cm,气体的温度T0=300K,压强为大气压强p0.现对气体缓慢加热,当气体温度升高到360K时,活塞(及铁砂)开始离开卡环而上升,此后在维持温度不变的条件下缓慢取走铁砂.已知活塞的横截面积是20cm2,大气压强p0为1×105 Pa,不计活塞与气缸之间的摩擦.求:
如图所示,一个质量可不计的活塞将一定量的理想气体封闭在上端开口的直立圆筒形气缸内,活塞上堆放着铁砂,最初活塞搁置在气缸内壁的固定卡环上,气体柱的高度为H0=10cm,气体的温度T0=300K,压强为大气压强p0.现对气体缓慢加热,当气体温度升高到360K时,活塞(及铁砂)开始离开卡环而上升,此后在维持温度不变的条件下缓慢取走铁砂.已知活塞的横截面积是20cm2,大气压强p0为1×105 Pa,不计活塞与气缸之间的摩擦.求:

