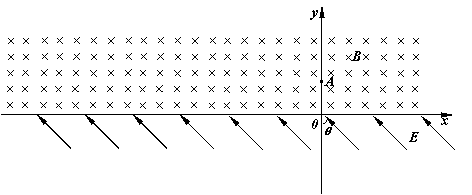��Ŀ����
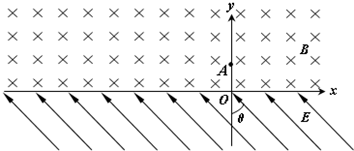
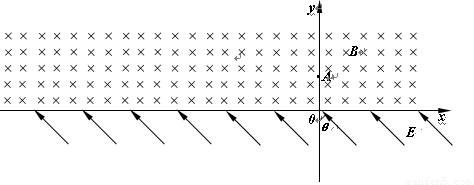
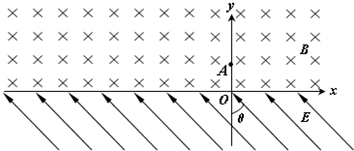
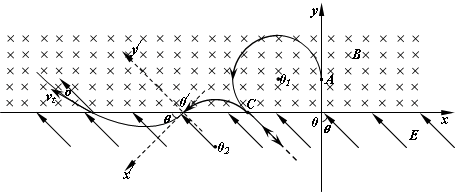
����ͼ��ʾ��x���Ϸ���һ��ǿ�ų����Ÿ�Ӧǿ�ȵķ���ֱ��ֽ�������СΪB��x���·���һ��ǿ�糡���糡ǿ�ȵĴ�СΪE��������y��ļнǦ�Ϊ45����б���Ϸ�������һ����Ϊm������Ϊq�������ӣ����ٶ�v0��y���ϵ�A����y������������ų����������ڴų����˶�һ��ʱ����x���ϵ�C�����糡�������Ӿ�C��ʱ���ٶȷ�����x��н�Ϊ45�㣮�������ӵ���������ų�����͵糡�����㹻�� ��
��1��C������ꣻ
��2�����Ӵ�A������������δ�Խx��ʱ���˶�ʱ�䣻
��3�����ӵ��Ĵδ�Խx��ʱ�ٶȵĴ�С���ٶȷ�����糡����ļнǣ�
��1��C������ꣻ
��2�����Ӵ�A������������δ�Խx��ʱ���˶�ʱ�䣻
��3�����ӵ��Ĵδ�Խx��ʱ�ٶȵĴ�С���ٶȷ�����糡����ļнǣ�

��1���ų��д�����������������������������Բ���˶�������qvB=m
�� r=
�����˶��켣��ͼ��ʾ���ɼ���֪ʶ֪��
xc=-(r+rcos45o)=-
��C��������-
��0��
��2��T=
�����Ӵ�A��C��ʱ��Ϊt1���ɼ���֪ʶ֪��t1=
T=
�����Ӵӽ���糡������C��ʱ��Ϊt2�����ڵ糡�����ȱ����˶�����ţ�ٵڶ����ɺ��˶�ѧ��ʽ����
qE=ma ��2v0=at2
������6����7����� t2=
�������ٴν���ų����ڴų����˶���ʱ��Ϊt3��������֪t3=
T=
�������Ӵ�A�㵽�����δ�Խx���ʱ��Ϊt=t1+t2+t3=
+
��3�����Ӵӵ����ι�x�ᵽ���Ĵι�x��Ĺ������ڵ糡������ƽ���˶���������v0�ķ�����Ϊx���ᣩ��v0�������˶�������qE�ķ�����Ϊy���ᣩ�����ٶ�Ϊ0���ȼ����˶�
��x'=v0t
y��=
t2
vy��=
t
�����ӵ��Ĵδ�Խx��ʱ�ٶȵĴ�СΪv���ٶȷ�����糡����ļн�Ϊ����
��ͼ�м��ι�ϵ֪
=cos450
=cos45�㣬v=
��tan��=
�ۺ�������v=
v0����=arctan
�𣺣�1��C��������ǣ�-
��0����
��2�����Ӵ�A������������δ�Խx��ʱ���˶�ʱ����
+
��
��3�����ӵ��Ĵδ�Խx��ʱ�ٶȵĴ�СΪ
v0���ٶȷ�����糡����ļн���=arctan
��
| v2 |
| r |
| mv |
| qB |

�����˶��켣��ͼ��ʾ���ɼ���֪ʶ֪��
xc=-(r+rcos45o)=-
(2+
| ||
| 2qB |
��C��������-
(2+
| ||
| 2qB |
��2��T=
| 2��m |
| qB |
�����Ӵ�A��C��ʱ��Ϊt1���ɼ���֪ʶ֪��t1=
| 5 |
| 8 |
| 5 |
| 4 |
| ��m |
| qB |
�����Ӵӽ���糡������C��ʱ��Ϊt2�����ڵ糡�����ȱ����˶�����ţ�ٵڶ����ɺ��˶�ѧ��ʽ����
qE=ma ��2v0=at2
������6����7����� t2=
| 2mv0 |
| qE |
�������ٴν���ų����ڴų����˶���ʱ��Ϊt3��������֪t3=
| 1 |
| 4 |
| ��m |
| 2qB |
�������Ӵ�A�㵽�����δ�Խx���ʱ��Ϊt=t1+t2+t3=
| 7��m |
| 4qB |
| 2mv0 |
| qE |
��3�����Ӵӵ����ι�x�ᵽ���Ĵι�x��Ĺ������ڵ糡������ƽ���˶���������v0�ķ�����Ϊx���ᣩ��v0�������˶�������qE�ķ�����Ϊy���ᣩ�����ٶ�Ϊ0���ȼ����˶�
��x'=v0t
y��=
| 1 |
| 2 |
| qE |
| m |
vy��=
| qE |
| m |
�����ӵ��Ĵδ�Խx��ʱ�ٶȵĴ�СΪv���ٶȷ�����糡����ļн�Ϊ����
��ͼ�м��ι�ϵ֪
| y�� |
| x�� |
| y�� |
| x�� |
|
| v0 |
| vy�� |
�ۺ�������v=
| 5 |
| 1 |
| 2 |
�𣺣�1��C��������ǣ�-
(2+
| ||
| 2qB |
��2�����Ӵ�A������������δ�Խx��ʱ���˶�ʱ����
| 7��m |
| 4qB |
| 2mv0 |
| qE |
��3�����ӵ��Ĵδ�Խx��ʱ�ٶȵĴ�СΪ
| 5 |
| 1 |
| 2 |

��ϰ��ϵ�д�
 ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д�
ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д� Сѧ������ҵϵ�д�
Сѧ������ҵϵ�д� ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�
�����Ŀ