题目内容
15.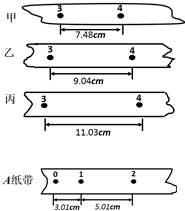 某同学测定匀变速直线运动的加速度时,得到了在不同拉力作用下的A、B、C…几条较为理想的纸带,并在这些纸带上每5个点取一个计数点,即相邻两计数点间的时间间隔为0.1s,将每条纸带上的计数点都记为0、1、2、3、4、5…..
某同学测定匀变速直线运动的加速度时,得到了在不同拉力作用下的A、B、C…几条较为理想的纸带,并在这些纸带上每5个点取一个计数点,即相邻两计数点间的时间间隔为0.1s,将每条纸带上的计数点都记为0、1、2、3、4、5…..(1)打点计时器打A纸带中1号计数点时小车的速度为0.40m/s.
(2)打A纸带时,物体的加速度大小是2.0m/s2. (前面两空计算结果保留两位有效数字)
(3)如图所示的甲、乙、丙三段纸带,分别是从其中三条不同纸带上撕下的.在甲、乙、丙三段纸带中,属于纸带A的是甲(填“甲”、“乙”,或“丙”).
分析 根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上1点时小车的瞬时速度大小.
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小.
解答 解:(1)纸带上每5个点取一个计数点,所以相邻的计数点间的时间间隔T=0.1s,
利用匀变速直线运动的推论
v1=$\frac{0.0301+0.0501}{2×0.1}$=0.40m/s
(2)根据运动学公式△x=at2得:
a=$\frac{0.00501-0.00301}{0.{1}^{2}}$m/s2=2.0m/s2
(3)根据匀变速直线运动的特点(相邻的时间间隔位移之差相等)得出:
x34-x23=x23-x12=x12-x01
所以属于纸带A的是甲图.
故答案为:(1)0.40;(2)2.0;(3)甲.
点评 要提高应用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用.

练习册系列答案
相关题目
5.若地球绕太阳公转周期及其公转轨道半径分别为T和R,月球绕地球公转周期和公转半径分别为t和r,则太阳质量与地球质量之比为( )
| A. | $\frac{{R}^{3}{t}^{2}}{{r}^{3}{T}^{2}}$ | B. | $\frac{{R}^{3}{T}^{2}}{{r}^{3}{t}^{2}}$ | C. | $\frac{{R}^{3}{t}^{2}}{{r}^{2}{T}^{3}}$ | D. | $\frac{{R}^{2}{T}^{3}}{{r}^{2}{t}^{3}}$ |
6.一质量为2kg的滑块,以2m/s的速度在光滑水平面上向右滑行,从某一时刻起,在滑块上作用一向右的水平力,经过2s,滑块的速度大小变为4m/s,则在这段时间里水平力对滑块所做的功为( )
| A. | 4J | B. | 8J | C. | 12J | D. | 16J |
20.下列关于物理学研究方法的叙述中,正确的是( )
| A. | 用比值定义法定义的物理概念在物理学中占有相当大的比例,例如v=$\frac{x}{t}$,a=$\frac{F}{m}$和P=$\frac{W}{t}$都是采用比值定义法定义的 | |
| B. | 伽利略为研究落体运动的特点所做的斜面实验运用了理想化模型的方法 | |
| C. | 根据速度定义式v=$\frac{△x}{△t}$,当△t非常小时,$\frac{△x}{△t}$就可以表示物体在t时刻的瞬时速度,该定义运用了理想化模型的方法 | |
| D. | 在推导弹簧弹力做功表达式时,把整个运动过程分成很多小段,每一小段近似看做恒力做功,再把各小段做功相加,这里运用了假设法 |
7.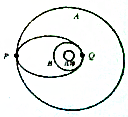 如图所示,“嫦娥二号”卫星在月球引力作用下,先在轨道A绕月球做匀速圆周运动,轨道A距月球表面的高度为hA,运动的周期为TA,在P和Q处两次变轨后最终进入绕月球做匀速圆周运动的轨道B,轨道B距月球表面的高度为hB,运动的周期为TB,已知引力常量为G,仅利用以上条件可求出( )
如图所示,“嫦娥二号”卫星在月球引力作用下,先在轨道A绕月球做匀速圆周运动,轨道A距月球表面的高度为hA,运动的周期为TA,在P和Q处两次变轨后最终进入绕月球做匀速圆周运动的轨道B,轨道B距月球表面的高度为hB,运动的周期为TB,已知引力常量为G,仅利用以上条件可求出( )
 如图所示,“嫦娥二号”卫星在月球引力作用下,先在轨道A绕月球做匀速圆周运动,轨道A距月球表面的高度为hA,运动的周期为TA,在P和Q处两次变轨后最终进入绕月球做匀速圆周运动的轨道B,轨道B距月球表面的高度为hB,运动的周期为TB,已知引力常量为G,仅利用以上条件可求出( )
如图所示,“嫦娥二号”卫星在月球引力作用下,先在轨道A绕月球做匀速圆周运动,轨道A距月球表面的高度为hA,运动的周期为TA,在P和Q处两次变轨后最终进入绕月球做匀速圆周运动的轨道B,轨道B距月球表面的高度为hB,运动的周期为TB,已知引力常量为G,仅利用以上条件可求出( )| A. | 月球表面的重力加速度 | |
| B. | 月球的质量和平均密度 | |
| C. | 月球自转周期 | |
| D. | 卫星在轨道A上运动的速率大于在轨道B上运动的速率 |
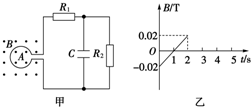 如图甲所示,截面积为0.2m2的100匝圆形线圈A处在变化的磁场中.磁场方向垂直纸面,其磁感应强度B随时间t的变化规律如图乙所示,设向外为B的正方向.R1=4Ω,R2=6Ω,线圈的内阻不计,
如图甲所示,截面积为0.2m2的100匝圆形线圈A处在变化的磁场中.磁场方向垂直纸面,其磁感应强度B随时间t的变化规律如图乙所示,设向外为B的正方向.R1=4Ω,R2=6Ω,线圈的内阻不计,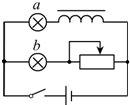 如图所示,a、b灯是两个完全相同的电灯,电路导通时,调节R,使a、b都正常发光.先断开开关,再闭合电键瞬间看到两灯没有同时发光,请判断b灯比a灯先发光,原因是:闭合开关瞬间,线圈电流瞬间增加,产生自感电动势,阻碍电流增加,因此a灯这一支路的电流就会延迟一段时间达到稳定值..
如图所示,a、b灯是两个完全相同的电灯,电路导通时,调节R,使a、b都正常发光.先断开开关,再闭合电键瞬间看到两灯没有同时发光,请判断b灯比a灯先发光,原因是:闭合开关瞬间,线圈电流瞬间增加,产生自感电动势,阻碍电流增加,因此a灯这一支路的电流就会延迟一段时间达到稳定值..