Question

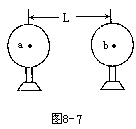
如图8-7所示，两个质量均为m的完全相同的金属球壳a与b，其壳层的厚度和质量分布均匀，将它们固定于绝缘支座上，两球心间的距离为L，为球半径的3倍。若使它们带上等量异种电荷，使其电量的绝对值均为Q，那么，a、b两球之间的万有引力F_引库仑力F_库分别为：

　　

Answer 1

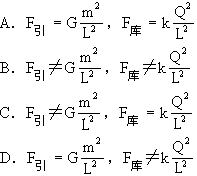
　　【错解分析】错解：

　　（1）因为a，b两带电球壳质量分布均匀，可将它们看作质量集中在球心的质点，也可看作点电荷，因此，万有引力定律和库仑定律对它们都适用，故其正确答案应选A。

　　（2）依题意，a，b两球中心间的距离只有球半径的3倍，它们不能看作质点，也不能看作点电荷，因此，既不能用万有引力定律计算它们之间的万有引力，也不能用库仑定律计算它们之间的静电力，故其正确答案应选B。

　　由于一些同学对万有引力定律和库仑定律的适用条件理解不深刻，产生了上述两种典型错解，因库仑定律只适用于可看作点电荷的带电体，而本题中由于a，b两球所带异种电荷的相互吸引，使它们各自的电荷分布不均匀，即相互靠近的一侧电荷分布比较密集，又因两球心间的距离L只有其半径r的3倍，不满足L＞＞r的要求，故不能将两带电球壳看成点电荷，所以不能应用库仑定律。

　　【正确解答】

　　万有引力定律适用于两个可看成质点的物体，虽然两球心间的距离L只有其半径r的3倍，但由于其壳层的厚度和质量分布均匀，两球壳可看作质量集中于球心的质点。因此，可以应用万有引力定律。