题目内容
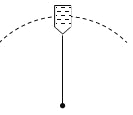
【题目】一细杆与水桶相连,水桶中装有水,水桶与细杆一起在竖直平面内做圆周运动,如图所示,水的质量m=0.5kg,水的重心到转轴的距离l=50cm。(取g=10m/s2,不计空气阻力)

⑴若在最高点水不流出来,求桶的最小速率;
⑵若在最高点水桶的速率v=3m/s,求水对桶底的压力。
【答案】⑴桶的最小速率为2.42m/s;⑵水对桶底的压力为5N
【解析】试题分析:分别以水桶和桶中的水为研究对象,对它们进行受力分析,找出它们做圆周运动所需向心力的来源,根据牛顿运动定律建立方程即解。
⑴以水桶中的水为研究对象,在最高点恰好不流出来,说明水
的重力恰好提供其做圆周运动所需的向心力,此时桶的速率最小。
此时有:
mg=m![]() ; 则所求的最小速率为:v0=
; 则所求的最小速率为:v0=![]() =
=![]() m/s=2.42m/s
m/s=2.42m/s
⑵在最高点,水所受重力mg的方向竖直向下,此时水具有向下的向心加速度,处于失重状态,其向心加速度的大小由桶底对水的压力和水的重力决定。
由向心力公式F=m![]() 可知,当v增大时,物体做圆周运动所需的向心力也随之增大,由于
可知,当v增大时,物体做圆周运动所需的向心力也随之增大,由于
v=3m/s>v0=2.42m/s,因此,当水桶在最高点时,水所受重力已不足以水做圆周运动所需的向心力,
此时桶底对水有一向下的压力,
设为FN,则由牛顿第二定律有:
FN+mg=m![]() ; ∴FN=m
; ∴FN=m![]() -mg
-mg
代入数据可得FN=5N。

练习册系列答案
相关题目