题目内容
13.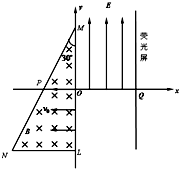 如图所示,在xOy平面直角坐标系中,直角三角形MNL内存在垂直于xOy平面向里磁感应强度为B的匀强磁场,三角形的一直角边ML长为6a,落在y轴上,∠NML=30°,其中位线OP在x轴上.电子束以相同的速度v0从y轴上-3a≤y≤0的区间垂直于y轴和磁场方向射入磁场,已知从y轴上y=-2a的点射入磁场的电子在磁场中的轨迹恰好经过O点.若在直角坐标系xOy的第一象限区域内,加上方向沿y轴正方向、大小为E=Bv0的匀强电场,在x=3a处垂直于x轴放置一平面荧光屏,与x轴交点为Q忽略电子间的相互作用,不计电子的重力.试求:
如图所示,在xOy平面直角坐标系中,直角三角形MNL内存在垂直于xOy平面向里磁感应强度为B的匀强磁场,三角形的一直角边ML长为6a,落在y轴上,∠NML=30°,其中位线OP在x轴上.电子束以相同的速度v0从y轴上-3a≤y≤0的区间垂直于y轴和磁场方向射入磁场,已知从y轴上y=-2a的点射入磁场的电子在磁场中的轨迹恰好经过O点.若在直角坐标系xOy的第一象限区域内,加上方向沿y轴正方向、大小为E=Bv0的匀强电场,在x=3a处垂直于x轴放置一平面荧光屏,与x轴交点为Q忽略电子间的相互作用,不计电子的重力.试求:(1)电子的比荷;
(2)电子束从+y轴上射入电场的纵坐标范围;
(3)从磁场中垂直于y轴射入电场的电子打到荧光屏上距Q点的最远距离.
分析 (1)从y轴上y=-2a点射入磁场的电子在磁场中的轨迹恰好经过O点,则电子圆周运动的半径为a,根据牛顿第二定律列方程求比荷;
(2)(3)粒子在磁场中运动圆轨迹必须与直线MN相切时打到荧光屏上距Q点最远.
解答 解:(1)由题意可知电子在磁场中的轨迹半径为r=a,
由牛顿第二定律得:ev0B=m$\frac{{v}_{0}^{2}}{r}$,
电子的比荷:$\frac{e}{m}$=$\frac{{v}_{0}}{Ba}$;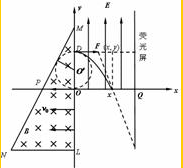 (2)电子能进入电场中,且离O点上方最远,电子在磁场中运动圆轨迹恰好与边MN相切,电子运动轨迹的圆心为O′点,如图所示.
(2)电子能进入电场中,且离O点上方最远,电子在磁场中运动圆轨迹恰好与边MN相切,电子运动轨迹的圆心为O′点,如图所示.
则:O′M=2a,OO′=OM-0′M=a,
即粒子从D点离开磁场进入电场时,离O点上方最远距离为:
OD=ym=2a,
所以电子束从y轴射入电场的范围为0≤y≤2a;
(3)假设电子没有射出电场就打到荧光屏上,
有 3a=v0t,y=$\frac{1}{2}$•$\frac{eE}{m}$•t2,
解得:y=$\frac{9}{2}$a>2a,所以,电子应射出电场后打到荧光屏上.
电子在电场中做类平抛运动,设电子在电场的运动时间为t,竖直方向位移为y,水平位移为x,
水平:x=v0t,竖直:y=$\frac{1}{2}$•$\frac{eE}{m}$•t2,
代入数据解得:x=$\sqrt{2ay}$;
设电子最终打在光屏的最远点距Q点为H,电子射出电场时的夹角为θ有:
tanθ=$\frac{{v}_{y}}{{v}_{x}}$=$\frac{\frac{eE}{m}×\frac{x}{{v}_{0}}}{{v}_{0}}$=$\sqrt{\frac{2y}{a}}$,
H=(3a-x)tanθ=(3$\sqrt{a}$-$\sqrt{2y}$)$\sqrt{2y}$,
当3$\sqrt{a}$-$\sqrt{2y}$=$\sqrt{2y}$时,即y=$\frac{9}{8}$a时,H有最大值,
由于$\frac{9}{8}$a<2a,所以Hmax=$\frac{9}{4}$a;
答:(1)电子的比荷为$\frac{{v}_{0}}{Ba}$;
(2)电子束从+y轴上射入电场的纵坐标范围是0≤y≤2a;
(3)从磁场中垂直于y轴射入电场的电子打到荧光屏上距Q点的最远距离为$\frac{9}{4}$a.
点评 本题属于带电粒子在组合场中的运动,粒子在磁场中做匀速圆周运动,要求能正确的画出运动轨迹,并根据几何关系确定某些物理量之间的关系;
粒子在电场中的偏转经常用化曲为直的方法,求极值的问题一定要先找出临界的轨迹,注重数学方法在物理中的应用.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案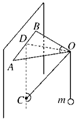 如图所示,A、B为竖直墙面上等高的两点,AO、BO为长度相等的两根轻绳,CO为一根轻杆,转轴C在AB中点D的正下方,AOB在同一水平面内,∠AOB=120°,∠COD=60°,若在O点处悬挂一个质量为m的物体,则平衡后绳AO所受的拉力和杆OC所受的压力分别为( )
如图所示,A、B为竖直墙面上等高的两点,AO、BO为长度相等的两根轻绳,CO为一根轻杆,转轴C在AB中点D的正下方,AOB在同一水平面内,∠AOB=120°,∠COD=60°,若在O点处悬挂一个质量为m的物体,则平衡后绳AO所受的拉力和杆OC所受的压力分别为( )| A. | mg,$\frac{1}{2}$mg | B. | $\frac{2\sqrt{3}}{3}$mg,$\frac{2\sqrt{3}}{3}$mg | C. | $\frac{1}{2}$mg,mg | D. | $\frac{\sqrt{3}}{3}$mg,$\frac{2\sqrt{3}}{3}$mg |
| A. | 光速不变原理指出光在真空中传播速度在不同惯性参考系中都是相同的 | |
| B. | 变化的电场一定产生变化的磁场,变化的磁场一定产生变化的电场 | |
| C. | 在光的双缝干涉实验中,若仅将入射光由红光改为绿光,则干涉条纹间距变宽 | |
| D. | 声源与观察者相对靠近时,观察者所接收的频率小于声源振动的频率 |
| A. | 飞行试验器绕月球运行的周期为2π$\sqrt{\frac{R}{g}}$ | |
| B. | 飞行试验器工作轨道处的重力加速度为($\frac{R}{R+h}$)2g | |
| C. | 飞行试验器在工作轨道上的绕行速度为R$\sqrt{\frac{g}{R+h}}$ | |
| D. | 月球的平均密度为$\frac{3g}{4πGR}$ |
 趣味运动会上运动员手持网球拍托球沿水平面匀加速跑,设球拍和球的质量分别为M、m,球拍平面和水平面之间的夹角为θ,球拍与球保持相对静止,它们间摩擦及空气阻力不计,则( )
趣味运动会上运动员手持网球拍托球沿水平面匀加速跑,设球拍和球的质量分别为M、m,球拍平面和水平面之间的夹角为θ,球拍与球保持相对静止,它们间摩擦及空气阻力不计,则( )| A. | 运动员的加速度为gtanθ | |
| B. | 球拍对球的作用力为$\frac{mg}{sinθ}$ | |
| C. | 运动员对球拍的作用力为$\frac{Mg}{cosθ}$ | |
| D. | 若加速度大于gsinθ,球一定沿球拍向上运动 |
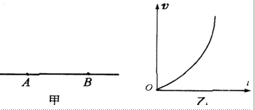 图甲是电场中一条电场线,A,B是电场线上的两点,一带正电粒子(只受电场力)沿直线从A点运动到B点的v-t图象如图乙所示,则关于A,B两点的电场强度EA和EB的下列说法正确的是( )
图甲是电场中一条电场线,A,B是电场线上的两点,一带正电粒子(只受电场力)沿直线从A点运动到B点的v-t图象如图乙所示,则关于A,B两点的电场强度EA和EB的下列说法正确的是( )| A. | 该电场一定是匀强电场 | |
| B. | EA<EB,电场方向从A向B | |
| C. | EA>EB,电场方向从A向B | |
| D. | 若该电场是由点电荷产生,在点电荷一定在B点的右方 |
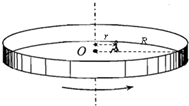 “魔盘”是一种神奇的游乐设施,它是一个能绕中心轴转动的带有竖直侧壁的大型转盘,随着“魔盘”转动角速度的增大,“魔盘”上的人可能滑向盘的边缘.如图所示,质量为m的人(视为质点)坐在转盘上,与转盘中心O相距r,转盘的半径为R,人与盘面及侧壁间的动摩擦因数均为μ,设最大静摩擦力等于滑动摩擦力,重力加速度为g.
“魔盘”是一种神奇的游乐设施,它是一个能绕中心轴转动的带有竖直侧壁的大型转盘,随着“魔盘”转动角速度的增大,“魔盘”上的人可能滑向盘的边缘.如图所示,质量为m的人(视为质点)坐在转盘上,与转盘中心O相距r,转盘的半径为R,人与盘面及侧壁间的动摩擦因数均为μ,设最大静摩擦力等于滑动摩擦力,重力加速度为g.
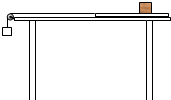 如图所示,一轻质薄木板静止在粗糙水平桌面,左端通过细绳跨过桌子边缘的定滑轮与重物相连,用手托住重物,细绳处于伸直状态.木板上有一质量为m=1kg的小铁块,它离木板的右端距离为L=0.5m,铁块与木板、木板与桌面间动摩擦因数为μ=0.1.释放重物,从静止开始以a0=2m/s2的加速度将木板从铁块下抽出,假设铁块大小、滑轮摩擦不计,桌面足够长,g取10m/s2,求:
如图所示,一轻质薄木板静止在粗糙水平桌面,左端通过细绳跨过桌子边缘的定滑轮与重物相连,用手托住重物,细绳处于伸直状态.木板上有一质量为m=1kg的小铁块,它离木板的右端距离为L=0.5m,铁块与木板、木板与桌面间动摩擦因数为μ=0.1.释放重物,从静止开始以a0=2m/s2的加速度将木板从铁块下抽出,假设铁块大小、滑轮摩擦不计,桌面足够长,g取10m/s2,求: