题目内容
 皮带运输机是靠货物和传送带间的摩擦力将货物送往高处,如图所示,已知传送带与水平面的倾角为θ=37°,以4m/s的速度匀速斜向上运行,在传送带的底部无初速的放上一个质为 0.5kg的物体,它与传送带间的动摩擦因数为0.8,传送带底部到顶端的长度为25m,则物体从底部到顶端的过程所用的时间是多少?物体机械能增加了多少?物体和传送带间产生的内能是多少?(sin37°=0.6,cos37°=0.8,g=10m/s2)
皮带运输机是靠货物和传送带间的摩擦力将货物送往高处,如图所示,已知传送带与水平面的倾角为θ=37°,以4m/s的速度匀速斜向上运行,在传送带的底部无初速的放上一个质为 0.5kg的物体,它与传送带间的动摩擦因数为0.8,传送带底部到顶端的长度为25m,则物体从底部到顶端的过程所用的时间是多少?物体机械能增加了多少?物体和传送带间产生的内能是多少?(sin37°=0.6,cos37°=0.8,g=10m/s2)分析:小球物体为研究对象,分析受力,根据牛顿第二定律求出开始阶段物体的加速度,由运动学公式求出物体速度增加到传送带相等时所需要的时间,以及通过的位移.物体到达最高点时,获得了动能与重力势能,两者的增量之和即为增加的机械能.物体和传送带间产生的内能等于摩擦力大小与两者相对位移乘积.
解答: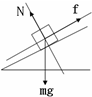 解:(1)开始时物体受力如图
解:(1)开始时物体受力如图
由牛顿第二定律知:
f-mgsinθ=ma…①
f=μN=μmgcosθ…②
由①②得:
a=μgcosθ-gsinθ═0.8×10×0.8-10×0.6=0.4m/s2
物体从0加速到4m/s,做匀加速运动
由vt=v0+at知:t=
=10s
∴S=
at2=
×0.4×102=20m.
由于还剩下5m做速度为4m/s的匀速运动,时间为1.25s.共用时间t总=11.25s.
(2)物体运动到最高得到的机械能E=mgh+
mv2=0.5×10×25×0.6+
0.5×42=79J
(3)产生的内能Q=f△S=μmgcosθ△S
△S=S带-S物=4×10-20=20m
∴Q=0.8×0.5×10×0.8×20=64J
答:物体从底部到顶端的过程所用的时间是11.25s.物体机械能增加了79J.物体和传送带间产生的内能是64J.
 解:(1)开始时物体受力如图
解:(1)开始时物体受力如图由牛顿第二定律知:
f-mgsinθ=ma…①
f=μN=μmgcosθ…②
由①②得:
a=μgcosθ-gsinθ═0.8×10×0.8-10×0.6=0.4m/s2
物体从0加速到4m/s,做匀加速运动
由vt=v0+at知:t=
| vt-v0 |
| a |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
由于还剩下5m做速度为4m/s的匀速运动,时间为1.25s.共用时间t总=11.25s.
(2)物体运动到最高得到的机械能E=mgh+
| 1 |
| 2 |
| 1 |
| 2 |
(3)产生的内能Q=f△S=μmgcosθ△S
△S=S带-S物=4×10-20=20m
∴Q=0.8×0.5×10×0.8×20=64J
答:物体从底部到顶端的过程所用的时间是11.25s.物体机械能增加了79J.物体和传送带间产生的内能是64J.
点评:对于传送带类型,关键分析物体的受力情况和运动情况,往往通过计算进行分析.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
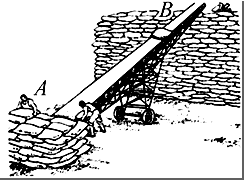 皮带运输机是靠货物和传送带之间的摩擦力把货物送往别处的.如图所示,已知传送带与水平面的倾角为θ=37°,以2m/s的速率向上运行,在传送带的底端A处无初速度地放上一质量为50kg的物体,它与传送带间的动摩擦因数为0.8.若传送带底端A到顶端B的长度为25m,则物体从A到B的时间为多少?(取g=10m/s2,sin 37°=0.6,cos 37°=0.8)
皮带运输机是靠货物和传送带之间的摩擦力把货物送往别处的.如图所示,已知传送带与水平面的倾角为θ=37°,以2m/s的速率向上运行,在传送带的底端A处无初速度地放上一质量为50kg的物体,它与传送带间的动摩擦因数为0.8.若传送带底端A到顶端B的长度为25m,则物体从A到B的时间为多少?(取g=10m/s2,sin 37°=0.6,cos 37°=0.8) 皮带运输机是靠货物和传送带之间的摩擦力把货物送往别处的.如图所示,已知传送带与水平面的倾角为θ=37°,以4m/s的速率向上运行,在传送带的底端A处无初速地放上一质量为0.5kg的物体,它与传送带间的动摩擦因数为0.8.若传送带底端A到顶端B的长度为25m,则物体从A到B的时间为多少?(取g=10m/s2,sin37°=0.6)
皮带运输机是靠货物和传送带之间的摩擦力把货物送往别处的.如图所示,已知传送带与水平面的倾角为θ=37°,以4m/s的速率向上运行,在传送带的底端A处无初速地放上一质量为0.5kg的物体,它与传送带间的动摩擦因数为0.8.若传送带底端A到顶端B的长度为25m,则物体从A到B的时间为多少?(取g=10m/s2,sin37°=0.6)
