题目内容
7.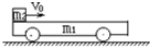 如图所示,质量m1=2kg的小车静止在光滑的水平面上,车长L=90m,现有质量m2=0.5kg可视为质点的物块,以水平向右的速度v0=20m/s从左端滑上小车,最后在车面上某处与小车保持相对静止.物块与车面间的动摩擦因数μ=0.4,取g=10m/s2,求:
如图所示,质量m1=2kg的小车静止在光滑的水平面上,车长L=90m,现有质量m2=0.5kg可视为质点的物块,以水平向右的速度v0=20m/s从左端滑上小车,最后在车面上某处与小车保持相对静止.物块与车面间的动摩擦因数μ=0.4,取g=10m/s2,求:(1)物块在车面上滑行的时间t;
(2)要使物块不从小车右端滑出,物块滑上小车左端的速度v0不超过多少.
分析 (1)根据动量守恒定律、动量定理物块在车面上滑行的时间t,首先判断动量是否守恒,再选取正方向列式求解;也可运用运动学公式和牛顿第二定律求解,对m2进行受力分析,求出加速,结合运动学公式v=v0+at可解出结果.
(2)根据动量守恒定律、能量守恒求解.也可运用牛顿第二定律求出物体和小车的加速度,由相对运动表示出出物块和小车的相对位移L,再结合运动学公式${{v}_{t}}^{2}-{{v}_{0}}^{2}=2as$可解出结果.
解答 解:
解法一:
(1)由题意知动量守恒,设物块与小车的共同速度为v,以水平向右为正方向(如图所示),根据动量守恒定律有
m2v0=(m1+m2)v…①
设物块与车面间的滑动摩擦力为F,对物块应用动量定理有
-Ft=m2v-m2v0…②
其中F=μm2g…③
解得 $t=\frac{{{m_1}{v_0}}}{{μ({{m_1}+{m_2}})g}}$
代入数据得 t=0.24s…④
(2)要使物块恰好不从车厢滑出,须物块到车面右端时与小车有共同的速度v′,则
m2v'0=(m1+m2)v'…⑤
由功能关系有$\frac{1}{2}{m_2}v'_0^2=\frac{1}{2}({{m_1}+{m_2}}){v'^2}+μ{m_2}gL$…⑥
⑤⑥联立并代入数据解得:v0′=5m/s
故要使物块不从小车右端滑出,物块滑上小车的速度v0′不能超过5m/s.
解法二:
(1)选物块原来的方向为正,
对小车有a1=$\frac{μ{m}_{2}g}{{m}_{1}}$=$\frac{10}{3}$m/s2,…①
对物块a2=$\frac{-μ{m}_{2}g}{{m}_{2}}$=-5m/s2…②
由于物块在车面上某处与小车保持相对静止,物块和车具有共同速度.
所以有v0+a2t=a1t…③
①②式代入③式解得t=0.24s
(2)要使物块恰好不从车厢滑出,须物块到车面最右端时与小车有共同的速度v′设小车的位移为s1,物块的位移为s2,物块原来的速度为v0'
对小车有:v′2-0=2a1s1…④
对物块有:${{v}^{′}}^{2}\;-\;{{v}_{0}^{′}}^{2}=2{a}_{2}{s}_{2}$…⑤
s2-s1=L…⑥
①②④⑤⑥联立解得v0'=5m/s
答:(1)物块在车面上滑行的时间为0.24s
(2)要使物块不从小车右端滑出,物块滑上小车左端的速度v0′不超过5m/s.
点评 本题考查摩擦拖动类的动量和能量问题,涉及动量守恒定律、动量定理、功能关系、牛顿第二定律和运动学公式这些物理规律的运用.本题采用了两种解法进行了求解,要注意明确两种解法的区别与联系,体会动量守恒定律解题的便捷性.

| A. | 加速下降 | B. | 加速上升 | C. | 减速上升 | D. | 减速下降 |
 某电场的电场线分布如图所示.A、B是同一条电场线上的两点,把一个正的试探电荷分别置于A、B两点的受力,以下说法正确的是( )
某电场的电场线分布如图所示.A、B是同一条电场线上的两点,把一个正的试探电荷分别置于A、B两点的受力,以下说法正确的是( )| A. | 大小相等,方向相同 | B. | 大小相等,方向不同 | ||
| C. | 大小不等,方向相同 | D. | 大小不等,方向不同 |

| A. | 两电阻的大小之比R1:R2为1:3 | B. | 两电阻的大小之比R1:R2为3:1 | ||
| C. | 两电阻丝长度之比为L1:L2=$\sqrt{3}$:1 | D. | 两电阻丝长度之比为L1:L2=1:$\sqrt{3}$ |
 跳水运动员从高台起跳跃入水中,运动员的重心运动的轨迹如图中虚线所示,则从起跳至入水的过程中,该运动员的重力势能的变化情况是( )
跳水运动员从高台起跳跃入水中,运动员的重心运动的轨迹如图中虚线所示,则从起跳至入水的过程中,该运动员的重力势能的变化情况是( )| A. | 一直减小 | B. | 一直增大 | C. | 先减小后增大 | D. | 先增大后减小 |
| A. | 测电压时,电流从红表笔流入多用电表,测电阻时,电流从红表笔流出多用电表 | |
| B. | 测电压时,电流从红表笔流出多用电表,测电阻时,电流从红表笔流入多用电表 | |
| C. | 选择欧姆档×10档并调零后,将两表笔与待测电阻相连,发现电表指针偏转角度太小,则应换用×100档,调零后再测 | |
| D. | 选择欧姆档的适当档位并调零后,将红表笔接二极管的正极,黑表笔接二极管的负极,可以测得二极管的反向电阻 |


