Question

【题目】一列沿x轴方向传播的横波，如图所示的实线和虚线分别为t1=0s时与t2=1s时的波形图像。求：

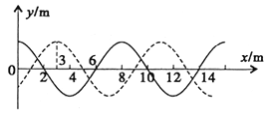
(i)如果该横波的传播速度为v=75m/s时，分析该波的传播方向；

(ii)如果该横波沿x轴的正方向传播，虚线上x=2m的质点到达平衡位置时波传播的最短距离是多少？相对应的时间应为多长？

Answer 1

【答案】(i)沿轴的正方向 (ii) 最短距离为 所用的时间应为(n＝0、1、2…)

【解析】

(1) 实线和虚线分别为t1=0s时与t2=1s时的波形图像，分沿x轴正方向和负方向传播两种情况分析处理；

(2) 横波沿x轴的正方向传播，找出最短距离的质点，再求出对应的时间。

(i) 如果沿轴的正方向传播，则的时间内，该波传播的距离为

Δs＝(nλ＋3)m＝(8n＋3)m(n＝0、1、2…)

若波速为，则1s的时间内波传播的距离为

则(8n＋3)=75，解得n＝9

显然波可能沿轴的正方向传播

如果沿轴的负方向传播，则的时间内，该波传播的距离为

Δs＝(nλ＋5)m＝(8n＋5)m(n＝0、1、2…)

若波速为则1s的时间内波传播的距离为

则(8n＋5)=75，解得

由于n必须为整数，则波不可能沿x轴的负方向传播

由以上可知，当波的速度为时，波的传播方向一定沿轴的正方向；

(ii) 图象可知：波长λ＝8m

当波沿x轴正向传播时，0~1s的时间内传播的距离：Δs＝(nλ＋3)m＝(8n＋3)m(n＝0、1、2…)

(8n＋3)m/s(n＝0、1、2…)

虚线上的质点到达平衡位置波应沿轴的正方向传播最短距离为

则所用的时间应为t (n＝0、1、2…)。